SciPy - Basic Functionality

SciPy is an open-source Python library that is widely used in the scientific community for various tasks involving numerical computation. This library is built on top of NumPy.

SciPy extends its capabilities by providing additional functionality that is essential for scientific and engineering applications. This includes algorithms and functions for optimization, integration, interpolation, eigenvalue problems and solving differential equations.

Here is the overview of the basic functionalities of SciPy library −

Numerical Integration

Numerical integration refers to techniques for calculating the integral of a function when an analytical solution is difficult or impossible to obtain. SciPy provides several methods for numerical integration as discussed below −

• Quad Integration: This is used to compute the integral of a function over a specified interval. In SciPy using scipy.integrate.quad() we can perform adaptive quadrature to compute definite integrals. It returns both the integral result and an estimate of the error.
• Simpsons Rule: This is a numerical method for estimating the definite integral of a function. It is particularly effective for integrating smooth functions and is based on approximating the function by a quadratic polynomial.

  This can be implemented by scipy.integrate.simps this method uses polynomial interpolation to provide a more accurate estimate than simple trapezoidal rules.

Example

Below is the example of computing the integral f(x) = e^-x2, which is the area under the curve of the Gaussian function and it converges to a known value by using the quad() function of the scipy.integrate module.

 from scipy import integrate import numpy as np # Function to integrate def f(x): return np.exp(-x**2) # Compute the integral from 0 to infinity result, error = integrate.quad(f, 0, np.inf) print(f"Integral result: {result}, Error estimate: {error}") 

Following is the output of the quad() function −

 Integral result: 0.8862269254527579, Error estimate: 7.101318378329813e-09 

Optimization

Optimization involves finding the best solution i.e. maximum or minimum of a given function. SciPy offers several optimization algorithms through the scipy.optimize(). Following are the methods that optimization can be done −

• Minimization: Use functions like minimize to find the minimum of a scalar function of one or more variables. It supports various methods such as Nelder-Mead, BFGS and Powell etc.
• Root Finding: The fsolve() function helps find the roots of a system of equations.

Example

The following example shows how to use the minimize() function of the scipy.optimize module to find the minimum of a simple quadratic function −

 from scipy import optimize # Define a function to minimize def objective_function(x): return (x - 2)**2 + 1 # Find the minimum of the function result = optimize.minimize(objective_function, x0=0) print(f"Minimum value: {result.fun} at x = {result.x}") 

Following is the output of the minimize() function −

 Minimum value: 1.0000000000000007 at x = [1.99999997] 

Interpolation

Interpolation is a technique to estimate unknown values that fall between known data points. SciPys scipy.interpolate module provides various methods for interpolation −

• Linear and Cubic Interpolation − Use interp1d for one-dimensional interpolation which can be linear, quadratic or cubic.
• Barycentric Interpolation − This provides high-order polynomial interpolation and is more numerically stable.

Example

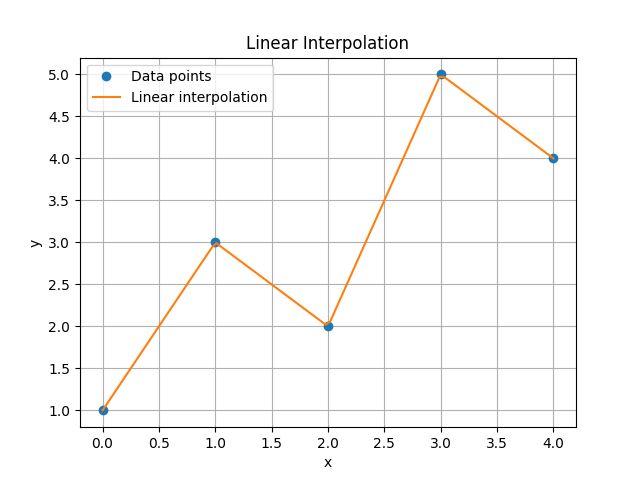
Here is the example which shows how to perform linear interpolation using SciPy and visualize the results with Matplotlib −

 from scipy import interpolate import matplotlib.pyplot as plt import numpy as np # Sample data x = np.array([0, 1, 2, 3, 4]) # Original x values y = np.array([1, 3, 2, 5, 4]) # Corresponding y values # Create a linear interpolation function linear_interp = interpolate.interp1d(x, y) # New x values for interpolation x_new = np.linspace(0, 4, 100) # 100 points between 0 and 4 y_new = linear_interp(x_new) # Interpolated y values # Plot the original data and the interpolation plt.plot(x, y, 'o', label='Data points') # Original data points as circles plt.plot(x_new, y_new, '-', label='Linear interpolation') # Interpolated line plt.legend() # Show legend plt.xlabel('x') plt.ylabel('y') plt.title('Linear Interpolation') plt.grid() # Add a grid plt.show() # Display the plot 

Following is the output of the Linear interpolation −

Eigenvalue Problems

Eigenvalue problems are a fundamental concept in linear algebra, arising in various fields such as physics, engineering, and data science. They involve finding eigenvalues and eigenvectors of a matrix. An eigenvalue and its corresponding eigenvector of a square matrix satisfy the equation as defined below −

Av = λv

Example

Below is the example which shows how to compute the eigenvalues and eigenvectors of a given matrix using the eig() function of the scipy.linalg module.

 from scipy.linalg import eig import numpy as np # Define a matrix A = np.array([[1, 2], [2, 1]]) # Compute eigenvalues and eigenvectors eigenvalues, eigenvectors = eig(A) print(f"Eigenvalues: {eigenvalues}") print(f"Eigenvectors:\n{eigenvectors}") 

Here is the output of the eigenvalues and eigenvectors of a given matrix −

 Eigenvalues: [ 3.+0.j -1.+0.j] Eigenvectors: [[ 0.70710678 -0.70710678] [ 0.70710678 0.70710678]] 

Algebraic Equations

SciPy provides tools for solving linear algebraic equations. The scipy.linalg module includes functions for matrix operations, solving linear systems and computing determinants.

Example

This is the example which shows how to use the solve() function of the scipy.linalg module on linear equations −

 import numpy as np from scipy.linalg import solve # Define a coefficient matrix A and a right-hand side vector b A = np.array([[3, 2], [1, 2]]) b = np.array([5, 5]) # Solve the linear system x = solve(A, b) print(f"Solution of the linear system: {x}") 

Following is the output of the above program −

 Solution of the linear system: [0. 2.5] 

Statistical Functions

SciPy also includes the scipy.stats module which contains a large collection of statistical distributions and functions for statistical testing.

• Probability Distributions: SciPy supports many continuous and discrete distributions such as normal, binomial, Poisson etc.
• Statistical Tests: There are functions for performing statistical tests such as t-tests and chi-square tests.

Example

This example shows how to perform a Shapiro-Wilk test for normality using the scipy.stats module in Python. This statistical test checks whether a given dataset follows a normal distribution −

 from scipy import stats import numpy as np # Generate random data data = np.random.normal(0, 1, 1000) # Perform a Shapiro-Wilk test for normality statistic, p_value = stats.shapiro(data) print(f"Shapiro-Wilk test statistic: {statistic}, p-value: {p_value}") 

Following is the output of the above program −

 Shapiro-Wilk test statistic: 0.9984066795076805, p-value: 0.49518026390115066