Discrete Mathematics Tutorial

Discrete Mathematics Tutorial

Discrete Mathematics is a branch of mathematics involving discrete elements that uses algebra and arithmetic. It is increasingly being applied in the practical fields of mathematics and computer science. It is a very good tool for improving reasoning and problem-solving capabilities. This tutorial explains the fundamental concepts of Sets, Relations and Functions, Mathematical Logic, Group theory, Counting Theory, Probability, Mathematical Induction and Recurrence Relations, Graph Theory, Trees and Boolean Algebra.

Branches of Discrete Mathematics

Following are the branches of discrete mathematics, each with its own set of concepts and applications:

• Set Theory − The study of collections of objects, including operations on sets and their properties.
• Logic − The study of reasoning and argumentation, including propositional and predicate logic.
• Combinatorics − Focuses on counting, arrangement, and combination of objects.
• Graph Theory − An essential field in computer science and mathematics that deals with graphs and their properties.
• Number Theory − The study of integers and their properties.
• Probability Theory − Deals with random events and their likelihood.
• Algebraic Structures − The study of abstract mathematical structures such as groups, rings, and fields.

Who Should Learn Discrete Mathematics

This tutorial has been prepared for students pursuing a degree in any field of computer science and mathematics. It has been published with a view to help students grasp the essential concepts of discrete mathematics.

Discrete mathematics plays an important role in algorithms, data structures, cryptography, and automata theory. It's a must for mathematics majors who need to have deep understanding of logic, combinatorics, and graph theory.

Discrete mathematics is equally important for Engineering Students, especially those in fields like electrical, computer, and software engineering, where digital logic, algorithm designing, network designing are needed.

Important topics like combinatorics, probability, and algorithm optimization are covered in discrete mathematics which are essential for data science. In addition, discrete Mathematics is vital for those professionals who work on formal reasoning and mathematical modeling, logics etc.

Prerequisites to Learn Discrete Mathematics

This tutorial has an ample amount of both theory and mathematics. The readers are expected to have a reasonably good understanding of elementary algebra and arithmetic.

• Basic Algebra − Understanding of algebraic operations and manipulation of equations.
• Logic − Familiarity with basic logical reasoning, truth tables, and conditional statements.
• Set Theory − A basic understanding of sets, subsets, and set operations.
• Functions and Relations − Basic knowledge of functions, mappings, and relations.
• Proof Techniques − Familiarity with mathematical proof methods like induction and contradiction.

Applications of Discrete Mathematics

Discrete mathematics provides tools for designing efficient algorithms and analysing their performance. For example, the time complexity of binary search is O(log n), which can be derived using concepts from discrete math.

Set theory and relational algebra, which are an integral part of discrete mathematics, form the basis of relational database systems. For example, SQL queries use set operations like UNION, INTERSECT, and EXCEPT.

Discrete Mathematics in Graph Theory and Computer Graphics

Discrete Mathematics plays an important role in Graph Theory and Computer Graphics.

Graph Theory

Discrete Mathematics provides the mathematical framework to study graphs, including concepts like vertices, edges, paths, and connectivity. Graph algorithms, such as those for traversals and shortest paths. These are needed for network design and optimization.

Graph theory comes under discrete mathematics that is extensively used in designing and analyzing computer networks. For example, shortest path algorithms like Dijkstra's algorithm use graph theory concepts.

Computer Graphics

Discrete mathematics helps in rendering, modeling, and animation. These techniques such as mesh generation, transformations, and shading rely on discrete geometric structures. Additionally, algorithms for collision detection and visibility uses graph-based methods.

Discrete geometry is used in computer graphics and image processing. For example, Bresenham's line algorithm uses concepts from discrete mathematics to efficiently draw lines on a pixel grid.

FAQs on Discrete Mathematics

In this section, we have collected a set of Frequently Asked Questions on Discrete Mathematics followed by their answers −

1. Difference between a Predicate and a Proposition

In simple terms, a proposition is a declarative statement. It is either true or false, but not both. For example, "The sky is blue" is a proposition because it has a clear truth value.

On the other hand, a predicate, is a statement that contains variables. It becomes a proposition when the variables are assigned specific values. For example, "x is greater than 5" is a predicate because its truth value depends on the value of x.

In short, propositions have fixed truth values but predicates depend on variables.

2. Difference between Injective, Surjective, and Bijective functions

In functions, the terms Injective, Surjective, and Bijective describe different mappings between sets −

• Injective (One-to-One) − A function is injective if each element in the domain maps to a unique element in the codomain. No two distinct elements share the same output.
• Surjective (Onto) − A function is surjective if every element in the codomain has at least one pre-image in the domain.
• Bijective − A function is bijective if it is both injective and surjective, meaning there is a one-to-one correspondence between the domain and codomain.

3. How are Venn diagrams used to solve Set Theory problems?

In Set Theory, Venn diagrams visually represent sets and their relationships. Each set is represented by a circle, with the universal set often shown as a rectangle.

Operations

• Union − Areas where circles overlap or combine represent the union of sets.
• Intersection − Overlapping regions show the common elements between sets.
• Complement − Areas outside a set’s circle represent the complement.
• Difference − Subtracting one set from another is shown by excluding overlapping regions.

4. What is the significance of De Morgans laws in Discrete Mathematics?

In set theory and Boolean algebra, we use De Morgan's laws. They represent how negations distribute over logical operations like conjunction (AND) and disjunction (OR):

• First Law ¬(A ∧ B) = ¬A ∨ ¬B
• Second Law ¬(A ∨ B) = ¬A ∧ ¬B

Significance

• Simplification − They help simplify complex logical expressions.
• Complementation − They are crucial in set theory, describing relationships between unions and intersections.
• Digital Logic − Used in circuit design to transform logic gates.

5. How does Proof by Contradiction work?

As the name suggests, Proof by Contradiction assumes the opposite of what we want to prove is true, and it leads to a contradiction.

• Assumption − Start by assuming the negation of the statement we want to prove. For example, if we want to prove P is true, assume P is false.
• Logical Deduction − Use logical reasoning and find facts to derive consequences from this assumption.
• Contradiction − Show that these consequences lead to a contradiction. They are logically inconsistent with known facts or the assumption itself.
• Conclusion − Since the assumption leads to a contradiction, we conclude that the original statement must be true.

6. What is Abstract Algebra? What is its relevance to cryptography?

Abstract Algebra is quite a common thing in mathematics. It is based on studies of algebraic structures like groups, rings, fields, and vectors. It focuses on underlying properties and operations (such as addition and multiplication) of these structures.

Abstract Algebra is used in Cryptography in the following ways −

• Group Theory − Cryptographic algorithms like RSA and Diffie-Hellman rely on group operations, particularly modular arithmetic and cyclic groups.
• Finite Fields − Fields like GF(2ⁿ) are used in encryption schemes, elliptic curve cryptography, and error-correcting codes.
• Security − The hardness of solving problems like discrete logarithms and factorization in these algebraic structures ensures cryptographic strength.

7. How does the Pigeonhole Principle apply to Computer Science problems?

The Pigeonhole Principle states that if n items are placed into m containers, and n > m, at least one container must hold more than one item.

Following are its applications in Computer Science:

• Hashing − In hash tables, the principle guarantees collisions if more elements than available hash values are inserted.
• Compression − It shows that not all data can be uniquely compressed, as there are fewer possible compressed outputs than inputs.
• Network Routing − It ensures that data packets may collide if more packets are sent than available paths.

8. What is the importance of Combinatorics in analyzing algorithm efficiency?

Combinatorics are useful in analyzing algorithm efficiency by:

• Counting − It helps to understand the number of possible inputs, outputs, or states an algorithm must handle. This is vital for understanding time complexity.
• Permutations and Combinations − Useful for analyzing problems involving searching, sorting, and optimization by understanding all possible configurations.
• Probability − Helps estimate the likelihood of certain outcomes in randomized algorithms or hashing.

9. How does Permutations differ from Combinations?

Permutations and Combinations differ based on order −

Permutations − Focus on arranging elements where the order matters. For n elements, the number of permutations of r elements is given by −

$$\mathrm{P(n,\: r)\: = \:\frac{n!}{(n \:-\: r)!}}$$

For example, arranging 3 letters from ABCD (ABC, ACB, etc.).

Combinations: Focus on selecting elements where order does not matter. The number of combinations of r elements from n is −

$$\mathrm{C(n,\: r) = \frac{n!}{r!(n \:-\: r)!}}$$

For example, selecting 3 letters from ABCD (ABC, ABD, etc.).

10. What is the role of Probability Theory in Computer Science?

Probability Theory are widely use in Computer Science −

• Randomized Algorithms − Probability helps get the expected performance of algorithms that make random choices, such as quicksort or Monte Carlo methods.
• Machine Learning − Probability Theory forms the basis for models like Naive Bayes and probabilistic inference in decision-making and classification tasks.
• Cryptography − Probability is used in assessing the security of encryption schemes and the likelihood of successful attacks.
• Error Detection − In networking and communication, probability is applied to error detection and correction techniques.

11. How are Conditional Probability and Bayes' Theorem used in AI?

Conditional Probability calculates the likelihood of an event occurring given the occurrence of another event. This is essential in AI for tasks like classification, decision-making, and prediction, where outcomes depend on prior events.

Bayes' Theorem updates the probability of a hypothesis based on new evidence. In AI, It is used in −

• Naive Bayes Classifiers − For spam detection, sentiment analysis, etc.
• Bayesian Networks − Modeling complex systems with interdependent variables.
• Decision Theory − For rational decision-making under uncertainty.

12. What are Generating Functions? How are they applied in Discrete Mathematics?

Generating functions are formal power series used to encode sequences of numbers, typically represented as −

$$\mathrm{G(x) \:=\: a_0 \:+\: a_1 x \:+\: a_2 x^2 \:+\: \dots}$$

Where a_n represents the coefficients of the series.

In discrete mathematics, generating functions are used in combinatorics to solve counting problems, find closed forms of sequences, and analyze recurrence relations. They help the manipulation of sequences through algebraic operations. It makes it easier to derive properties and relationships, such as finding the number of ways to arrange objects or solve partition problems.

13. How does Graph Theory relate to Network Design and Analysis?

In networking, graph theory is used to design and analysis, providing a mathematical framework to model relationships in networks. In this context −

• Vertices and Edges − Represent network nodes (e.g., computers, routers) and connections (e.g., cables, links).
• Pathfinding − Algorithms like Dijkstra's and A* help find the shortest paths for data transmission.
• Connectivity − Analyzing network robustness involves studying graph connectivity and components.
• Flow Networks − Techniques like the Ford-Fulkerson method optimize resource distribution.

14. Difference between Eulerian and Hamiltonian paths in Graph Theory

In Graph Theory, Eulerian and Hamiltonian paths are distinct concepts −

• Eulerian Path − A path that visits every edge of a graph exactly once. A graph has an Eulerian path if it has at most two vertices of odd degree. If all vertices have even degrees, it contains an Eulerian circuit.
• Hamiltonian Path − A path that visits every vertex exactly one. Unlike Eulerian paths, there is no specific degree conditions for Hamiltonian path, making them more complex to determining.

15. How Graph Coloring is applied in scheduling and resource allocation problems?

Graph coloring is a technique used in scheduling and resource allocation by representing tasks or resources as graph vertices, with edges indicating conflict or dependency.

Scheduling − In scheduling problems, colors represent time slots. A valid coloring gives that no two conflicting tasks (connected vertices) are assigned the same time slot, minimizing overlaps.

Resource Allocation − In resource allocation, graph coloring idea help allocate resources to tasks without conflicts, ensuring efficient utilization.

16. What are Planar Graphs? What is their importance in circuit design?

Planar graphs are graphs that can be drawn on a plane or a piece of paper without any edges crossing. This property is needed in various applications, particularly in circuit design.

In circuit design, planar graphs help represent electrical circuits and components efficiently. The wires (edges) do not intersect in a layout. It minimizes signal interference and makes circuits easier to manufacture.

Planarity simplifies the design processes. It allows for more effective routing and component placement. Ultimately leading for more compact and reliable circuit boards.

17. How does Number Theory apply to Cryptography and Computer Security?

Number theory is useful in cryptography and computer security. They are providing the mathematical foundations for secure communication.

Key applications include −

• Prime Numbers − Used in algorithms like RSA, where large primes enable secure key generation and encryption.
• Modular Arithmetic − Used for creating and deciphering encrypted messages, which operations comes within a finite sets.
• Discrete Logarithms − Form the basis for protocol Diffie-Hellman, allowing secure key exchange.

18. What are Diophantine Equations?

Diophantine equations are polynomial equations that find integer solutions. They take the form ax + by = c, where a, b, and c are integers.

The key characteristic is that solutions must be integers. Linear Diophantine equations have solutions if the greatest common divisor (GCD) of a and b divide c. These equations are important in number theory and have different applications in cryptography, algorithm design, and computer science.

19. What is big-O notation? What is its importance in Algorithm Analysis?

Big-O or Big-Oh notation is a mathematical notation to describe the upper bound of an algorithm's runtime or space requirements in terms of the size of the input.

Take a look at the following example −

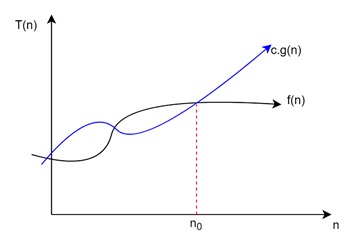
In this example, the function g(n) is upper bound for function f(n), so f(n) = O(g(n)).

20. How does Discrete Mathematics contribute to the design of Finite State Machines?

The concepts of Discrete Mathematics are used in several different ways in Finite State Machines (FSMs) and Automata Theory −

• Set Theory − Defines states, inputs, and outputs as sets.
• Graph Theory − Represents FSMs as directed graphs, where nodes are states and edges are transitions based on input.
• Logic − Uses logical expressions to define state transitions and output conditions, ensuring clear specifications.
• Combinatorics − Analyzes the number of possible states and transitions, crucial for optimizing design.

Take a look at the following example –

Here, the FSM can be defined with sets. For example, states V = {A, B, C, D}, similarly transitions too can be defined with sets.

21. How does Discrete Mathematics contribute to the study of Formal Languages and Automata Theory?

Discrete Mathematics covers some of the fundamental concepts of Automata Theory, such as −

• Set Theory − Defines languages as sets of strings, grammars, languages, closure properties, etc.
• Graph Theory − Models automata as graphs, with states as nodes and transitions as edges.
• Logic − Uses propositional and predicate logic to formalize language semantics.
• Proof Techniques − Applies techniques like induction to prove properties about languages and automata. Also pumping lemma for proofing with contradictions.

22. What is Mathematical Induction?

Mathematical Induction is a technique to prove some hypothesis which is used to establish the truth of an infinite number of cases. It has two conditions to prove −

• Base Case − Prove that a statement holds for the initial case, usually n = 1.
• Inductive Step − Assume the statement holds for n = k, and then prove it holds for n = k + 1.

Its applications in Algorithm Analysis are as follows −

• Correctness Proof − Induction is used to prove the correctness of recursive algorithms. It shows how they work for base and subsequent cases.
• Time Complexity − It helps to analyze the time complexity of recursive algorithms. This proves that they hold for all input sizes.