- ML - Home
- ML - Introduction
- ML - Getting Started
- ML - Basic Concepts
- ML - Ecosystem
- ML - Python Libraries
- ML - Applications
- ML - Life Cycle
- ML - Required Skills
- ML - Implementation
- ML - Challenges & Common Issues
- ML - Limitations
- ML - Reallife Examples
- ML - Data Structure
- ML - Mathematics
- ML - Artificial Intelligence
- ML - Neural Networks
- ML - Deep Learning
- ML - Getting Datasets
- ML - Categorical Data
- ML - Data Loading
- ML - Data Understanding
- ML - Data Preparation
- ML - Models
- ML - Supervised Learning
- ML - Unsupervised Learning
- ML - Semi-supervised Learning
- ML - Reinforcement Learning
- ML - Supervised vs. Unsupervised
- Machine Learning Data Visualization
- ML - Data Visualization
- ML - Histograms
- ML - Density Plots
- ML - Box and Whisker Plots
- ML - Correlation Matrix Plots
- ML - Scatter Matrix Plots
- Statistics for Machine Learning
- ML - Statistics
- ML - Mean, Median, Mode
- ML - Standard Deviation
- ML - Percentiles
- ML - Data Distribution
- ML - Skewness and Kurtosis
- ML - Bias and Variance
- ML - Hypothesis
- Regression Analysis In ML
- ML - Regression Analysis
- ML - Linear Regression
- ML - Simple Linear Regression
- ML - Multiple Linear Regression
- ML - Polynomial Regression
- Classification Algorithms In ML
- ML - Classification Algorithms
- ML - Logistic Regression
- ML - K-Nearest Neighbors (KNN)
- ML - Naïve Bayes Algorithm
- ML - Decision Tree Algorithm
- ML - Support Vector Machine
- ML - Random Forest
- ML - Confusion Matrix
- ML - Stochastic Gradient Descent
- Clustering Algorithms In ML
- ML - Clustering Algorithms
- ML - Centroid-Based Clustering
- ML - K-Means Clustering
- ML - K-Medoids Clustering
- ML - Mean-Shift Clustering
- ML - Hierarchical Clustering
- ML - Density-Based Clustering
- ML - DBSCAN Clustering
- ML - OPTICS Clustering
- ML - HDBSCAN Clustering
- ML - BIRCH Clustering
- ML - Affinity Propagation
- ML - Distribution-Based Clustering
- ML - Agglomerative Clustering
- Dimensionality Reduction In ML
- ML - Dimensionality Reduction
- ML - Feature Selection
- ML - Feature Extraction
- ML - Backward Elimination
- ML - Forward Feature Construction
- ML - High Correlation Filter
- ML - Low Variance Filter
- ML - Missing Values Ratio
- ML - Principal Component Analysis
- Reinforcement Learning
- ML - Reinforcement Learning Algorithms
- ML - Exploitation & Exploration
- ML - Q-Learning
- ML - REINFORCE Algorithm
- ML - SARSA Reinforcement Learning
- ML - Actor-critic Method
- ML - Monte Carlo Methods
- ML - Temporal Difference
- Deep Reinforcement Learning
- ML - Deep Reinforcement Learning
- ML - Deep Reinforcement Learning Algorithms
- ML - Deep Q-Networks
- ML - Deep Deterministic Policy Gradient
- ML - Trust Region Methods
- Quantum Machine Learning
- ML - Quantum Machine Learning
- ML - Quantum Machine Learning with Python
- Machine Learning Miscellaneous
- ML - Performance Metrics
- ML - Automatic Workflows
- ML - Boost Model Performance
- ML - Gradient Boosting
- ML - Bootstrap Aggregation (Bagging)
- ML - Cross Validation
- ML - AUC-ROC Curve
- ML - Grid Search
- ML - Data Scaling
- ML - Train and Test
- ML - Association Rules
- ML - Apriori Algorithm
- ML - Gaussian Discriminant Analysis
- ML - Cost Function
- ML - Bayes Theorem
- ML - Precision and Recall
- ML - Adversarial
- ML - Stacking
- ML - Epoch
- ML - Perceptron
- ML - Regularization
- ML - Overfitting
- ML - P-value
- ML - Entropy
- ML - MLOps
- ML - Data Leakage
- ML - Monetizing Machine Learning
- ML - Types of Data
- Machine Learning - Resources
- ML - Quick Guide
- ML - Cheatsheet
- ML - Interview Questions
- ML - Useful Resources
- ML - Discussion
Quantum Machine Learning With Python
Quantum Machine Learning (QML) can be effectively implemented using the Python programming language. The unique capabilities of python make it suitable for quantum machine learning. Researchers can combine the quantum mechanics principles with flexibility of Python libraries such as Qiskit and Cirq to develop and implement ML algorithms.
Researchers can explore novel approaches to solve complex problems in fields like drug discovery, financial modeling, etc., where traditional ML may fall short.
What is Quantum Machine Learning?
Quantum Machine Learning is an interdisciplinary research area that combines fields such as quantum computing, machine learning, optimization, etc. to improve the performance of machine learning models.
It applies unique capabilities of quantum computers to enhance the performance of machine learning algorithms. QML is capable of performing computations beyond the capabilities of conventional computers.
Why Python for Quantum Machine Learning?
There are many programming languages such as Python, Julia, C++, Q#, etc., that are being used for Quantum Machine Learning. But Python is the most popular among these programming languages.
Python is easy to learn and easy to implement machine learning algorithms for beginners as well as experienced.
Python provides many popular libraries and frameworks for quantum machine learning. Some popular ones include PennyLane, Qiskit, Cirq, etc.
Python also provides many scientific computing libraries such as SciPy, Pandas, Scikit-learn, etc. Python integrates these libraries with QML libraries.
Python Libraries/ Frameworks for Quantum Machine Learning
Python offers many libraries and frameworks that are currently being used for Quantum Machine Learning. The following are a few of important libraries -
- PennyLane − a popular and user-friendly library for building and training quantum machine learning models.
- Qiskit − it is a comprehensive quantum computing framework developed by IBM. It includes a dedicated module on QML. It provides various algorithms, simulators, etc., through the IBM cloud platform.
- Cirq − developed by Google, it is another powerful quantum computing framework that supports Quantum Machine Learning.
- TensorFlow Quantum (TFQ) minus; It is a quantum machine learning library for rapid prototyping of hybrid quantum-classical ML models.
- sQUlearn − it is a user-friendly library that integrates quantum machine learning with classical machine learning libraries or tools such as scikit-learn.
- PyQuil − It is developed by Rigetti Computing. It is a Python library for quantum programming and quantum machine learning. It provides tools for building and executing quantum circuits on Rigetti's quantum processors.
Quantum Machine Learning Program with Python
Python is a very versatile programming language that provides many libraries for Quantum Machine Learning. The main part of the QML is to design and execute quantum circuits.
With the help of Python libraries, the designing and execution of quantum circuits are easy.
We need a specific quantum machine learning library to implement a QML program in Python. In this section, we will use the PennyLane Python library for this purpose.
Prerequisites
The following are the prerequisites for implementation of quantum machine learning in Python -
- Programming Language: Python
- QML library: PennyLane
- Visualization Library: Matplotlib
Get started with PennyLane
We use the PennyLane Python library to implement the program below. It provides mechanisms to create and execute the quantum circuits. You can explore other Python libraries as well.
Before starting, you need to install the PennyLane library.
pip install pennylane
Steps
The following are the steps to perform a quantum machine learning program using Python -
- Install and import required libraries
- Prepare training and test data
- Define a quantum device. Specify the device type and the number of wires.
- Define the quantum circuit.
- Define pre-/post processing. Here we define the loss function to find total loss.
- Define a cost function which takes in your quantum circuit and loss function.
- Perform optimization
- Choose an optimizer.
- Define the step size.
- Initialize the parameters (make an initial guess for the value of parameters).
- Iterate over a number of defined steps.
- Test and Visualize the result.
Program Example
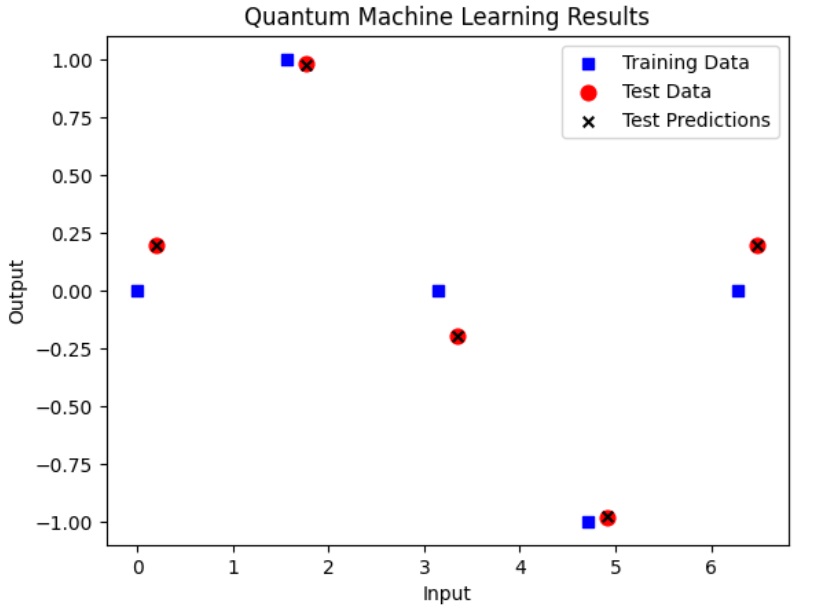
In the below example, we train a quantum circuit to model a sine function. We use the PennyLane Python library to define a quantum device and to create a quantum circuit. We use Gradient Descent optimizer as an optimization technique.
# Program to train a quantum circuit to model a sine function # Step 1- Import the necessary libraries import pennylane as qml from pennylane import numpy as np import matplotlib.pyplot as plt # Step 2 - Prepare the training data and test data # Training data preparation X = np.linspace(0, 2*np.pi, 5) # 5 input datapoints from 0 to 2pi X.requires_grad = False # Prevent optimization of input data Y = np.sin(X) # Corresponding outputs # Test data preparation X_test = np.linspace(0.2, 2*np.pi+0.2, 5) # 5 test datapoints Y_test = np.sin(X_test) # Corresponding outputs # Step 3 - Quantum device setup # Using 'default.qubit' simulator with 1 qubit dev = qml.device('default.qubit', wires=1) # Step 4 - Create the quantum circuit @qml.qnode(dev) def quantum_circuit(input_data, params): """ Quantum circuit to model the sine function. Args: input_data (float): Input data point. params (array): Parameters for the quantum gates. Returns: float: Expectation value of PauliZ measurement. """ # Encode the input data as an RX rotation qml.RX(input_data, wires=0) # Create a rotation based on the angles in "params" qml.Rot(params[0], params[1], params[2], wires=0) # We return the expected value of a measurement along the Z axis return qml.expval(qml.PauliZ(wires=0)) # Step 5 -Loss function definition def loss_func(predictions): total_losses = 0 for i in range(len(Y)): output = Y[i] prediction = predictions[i] loss = (prediction - output)**2 total_losses += loss return total_losses # Step 6 - Cost function definition def cost_fn(params): # Cost function to be minimized during optimization. predictions = [quantum_circuit(x, params) for x in X] cost = loss_func(predictions) return cost # Steps 7 - Optimization Step # Choose Gradient Descent Optimizer and step size as 0.3 opt = qml.GradientDescentOptimizer(stepsize=0.3) # initialize the parameters params = np.array([0.1,0.1,0.1],requires_grad=True) # iterate over a number of defined steps for i in range (100): params, prev_cost = opt.step_and_cost(cost_fn,params) if i%10 == 0: # print the result after every 10 steps print(f'Step {i} => Cost = {cost_fn(params)}') # Step 8 - # Testing and visualization test_predictions = [] for x_test in X_test: prediction = quantum_circuit(x_test,params) test_predictions.append(prediction) fig = plt.figure() ax1 = fig.add_subplot(111) ax1.scatter(X, Y, s=30, c='b', marker="s", label='Training Data') ax1.scatter(X_test,Y_test, s=60, c='r', marker="o", label='Test Data') ax1.scatter(X_test,test_predictions, s=30, c='k', marker="x", label='Test Predictions') plt.xlabel("Input") plt.ylabel("Output") plt.title("Quantum Machine Learning Results") plt.legend(loc='upper right'); plt.show() Output
Step 0 => Cost = 4.912499465469817 Step 10 => Cost = 0.01771261626471407 Step 20 => Cost = 0.0010549650559467845 Step 30 => Cost = 0.00033478390918249124 Step 40 => Cost = 0.00019081038150774426 Step 50 => Cost = 0.00012461609775915093 Step 60 => Cost = 8.781349557162982e-05 Step 70 => Cost = 6.52239822689053e-05 Step 80 => Cost = 5.0362401887345095e-05 Step 90 => Cost = 4.006386705383739e-05