Binomial Heaps

A binomial Heap is a collection of Binomial Trees. A binomial tree Bk is an ordered tree defined recursively. A binomial Tree B0 consists of a single node.

A binomial tree is an ordered tree defined recursively. A binomial tree Bk consists of two binomial trees Bk-1 that are linked together. The root of one is the leftmost child of the root of the other.

Binomial trees are defined recursively. A binomial tree B_k is defined as follows

• B₀ is a single node.

• B_k is formed by linking two binomial trees B_k-1 such that the root of one is the leftmost child of the root of the other.

Some properties of binomial trees are

• Binomial tree with B_k has 2_k nodes.

• Height of the tree is k

• There are exactly j! / (i! * (j-i)!) nodes at depth i for all i in range 0 to k.

What is Binomial Heap?

As mentioned above, a binomial heap is a collection of binomial trees. These binomial trees are linked together in a specific way. The binomial heap has the following properties

• Each binomial tree in the heap follows the min-heap property.

• No two binomial trees in the heap can have the same number of nodes.

• There is at most one binomial tree of any order.

Representation of Binomial Heap

Following is a representation of binomial heap, where B_k is a binomial heap of order k.

Some binomial heaps are like below

Example of Binomial Heap

This binomial Heap H consists of binomial trees B0, B2 and B3. Which have 1, 4 and 8 nodes respectively. And in total n = 13 nodes. The root of binomial trees are linked by a linked list in order of increasing degree

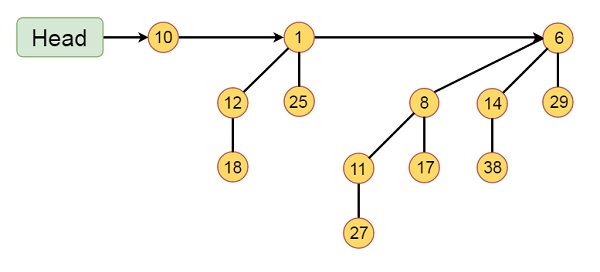
Operations on Binomial Heap

Following are the operations that can be performed on a binomial heap

• Insert: As name suggests, it is used to insert a node into the heap.

• Union: It is used to merge two binomial heaps into a single binomial heap.

• Extract-Min: This operation removes the node with the smallest key from the heap.

• Decrease-Key: This operation decreases the key of a node in the heap.

• Delete: Simply put, it deletes a node from the heap.

Implementation of Binomial Heap

We can implement a binomial heap using a linked list of binomial trees. Each node in the linked list is a binomial tree. The root of each binomial tree is the head of the linked list. The linked list is ordered by the order of the binomial trees. The binomial heap is the head of the linked list.

Implementation of binomial heap using following steps

 1. Create a new node with the given key. 2. Merge the new node with the binomial heap. 3. Adjust the binomial heap to maintain the heap property. 4. Insert the new node into the binomial heap. 5. Print the binomial heap. 

Code for Binomial Heap

Following is the implementation of binomial heap in C, C++, Java and Python.

In the following code, first we create a structure Node to represent a node in the binomial heap. The structure contains the data, degree, child, sibling, and parent of the node. We then define functions to create a new node, merge two binomial trees, union two binomial heaps, adjust the heap, and insert a new node into the heap. Finally, we print the binomial heap.

 #include <stdio.h> #include <stdlib.h> #include <limits.h> struct Node { int data, degree; struct Node *child, *sibling, *parent; }; struct Node *newNode(int key) { struct Node *temp = (struct Node *)malloc(sizeof(struct Node)); temp->data = key; temp->degree = 0; temp->child = temp->parent = temp->sibling = NULL; return temp; } struct Node *mergeBinomialTrees(struct Node *b1, struct Node *b2) { if (b1->data > b2->data) { struct Node *temp = b1; b1 = b2; b2 = temp; } b2->parent = b1; b2->sibling = b1->child; b1->child = b2; b1->degree++; return b1; } struct Node *unionBinomialHeap(struct Node *h1, struct Node *h2) { if (!h1) return h2; if (!h2) return h1; struct Node *newHeap = NULL, **pos = &newHeap; struct Node *curr1 = h1, *curr2 = h2; while (curr1 && curr2) { if (curr1->degree <= curr2->degree) { *pos = curr1; curr1 = curr1->sibling; } else { *pos = curr2; curr2 = curr2->sibling; } pos = &((*pos)->sibling); } *pos = (curr1) ? curr1 : curr2; return newHeap; } struct Node *adjustHeap(struct Node *head) { if (!head) return NULL; struct Node *prev = NULL, *curr = head, *next = head->sibling; while (next) { if (curr->degree != next->degree || (next->sibling && next->sibling->degree == curr->degree)) { prev = curr; curr = next; } else { if (curr->data <= next->data) { curr->sibling = next->sibling; curr = mergeBinomialTrees(curr, next); } else { if (!prev) head = next; else prev->sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr->sibling; } return head; } struct Node *insert(struct Node *heap, int key) { struct Node *temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } void printTree(struct Node *h) { while (h) { printf("%d ", h->data); printTree(h->child); h = h->sibling; } } void printHeap(struct Node *h) { printf("Binomial Heap: \n"); while (h) { printf("B%d: ", h->degree); printTree(h); printf("\n"); h = h->sibling; } } int main() { struct Node *hp = NULL; hp = insert(hp, 10); hp = insert(hp, 20); hp = insert(hp, 30); hp = insert(hp, 40); printHeap(hp); return 0; } 

 10 20 30 40 

 #include <iostream> #include <limits.h> using namespace std; struct Node { int data, degree; Node *child, *sibling, *parent; }; Node *newNode(int key) { Node *temp = new Node; temp->data = key; temp->degree = 0; temp->child = temp->parent = temp->sibling = NULL; return temp; } Node *mergeBinomialTrees(Node *b1, Node *b2) { if (b1->data > b2->data) { Node *temp = b1; b1 = b2; b2 = temp; } b2->parent = b1; b2->sibling = b1->child; b1->child = b2; b1->degree++; return b1; } Node *unionBinomialHeap(Node *h1, Node *h2) { if (!h1) return h2; if (!h2) return h1; Node *newHeap = NULL, **pos = &newHeap; Node *curr1 = h1, *curr2 = h2; while (curr1 && curr2) { if (curr1->degree <= curr2->degree) { *pos = curr1; curr1 = curr1->sibling; } else { *pos = curr2; curr2 = curr2->sibling; } pos = &((*pos)->sibling); } *pos = (curr1) ? curr1 : curr2; return newHeap; } Node *adjustHeap(Node *head) { if (!head) return NULL; Node *prev = NULL, *curr = head, *next = head->sibling; while (next) { if (curr->degree != next->degree || (next->sibling && next->sibling->degree == curr->degree)) { prev = curr; curr = next; } else { if (curr->data <= next->data) { curr->sibling = next->sibling; curr = mergeBinomialTrees(curr, next); } else { if (!prev) head = next; else prev->sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr->sibling; } return head; } Node *insert(Node *heap, int key) { Node *temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } void printTree(Node *h) { while (h) { cout << h->data << " "; printTree(h->child); h = h->sibling; } } void printHeap(Node *h) { cout << "Binomial Heap: " << endl; while (h) { cout << "B" << h->degree << ": "; printTree(h); cout << endl; h = h->sibling; } } int main() { Node *hp = NULL; hp = insert(hp, 10); hp = insert(hp, 20); hp = insert(hp, 30); hp = insert(hp, 40); printHeap(hp); return 0; } 

 10 20 30 40 

 import java.util.*; class Node { int data, degree; Node child, parent, sibling; } public class BinomialHeap { Node newNode(int key) { Node temp = new Node(); temp.data = key; temp.degree = 0; temp.child = temp.parent = temp.sibling = null; return temp; } Node mergeBinomialTrees(Node b1, Node b2) { if (b1.data > b2.data) { Node temp = b1; b1 = b2; b2 = temp; } b2.parent = b1; b2.sibling = b1.child; b1.child = b2; b1.degree++; return b1; } Node unionBinomialHeap(Node h1, Node h2) { if (h1 == null) return h2; if (h2 == null) return h1; Node dummy = new Node(); // Dummy node to track newHeap Node tail = dummy; Node curr1 = h1, curr2 = h2; while (curr1 != null && curr2 != null) { if (curr1.degree <= curr2.degree) { tail.sibling = curr1; curr1 = curr1.sibling; } else { tail.sibling = curr2; curr2 = curr2.sibling; } tail = tail.sibling; } tail.sibling = (curr1 != null) ? curr1 : curr2; return dummy.sibling; // Return merged heap without dummy node } Node adjustHeap(Node head) { if (head == null) return null; Node prev = null, curr = head, next = head.sibling; while (next != null) { if (curr.degree != next.degree || (next.sibling != null && next.sibling.degree == curr.degree)) { prev = curr; curr = next; } else { if (curr.data <= next.data) { curr.sibling = next.sibling; curr = mergeBinomialTrees(curr, next); } else { if (prev == null) head = next; else prev.sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr.sibling; } return head; } Node insert(Node heap, int key) { Node temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } void printTree(Node h) { while (h != null) { System.out.print(h.data + " "); printTree(h.child); h = h.sibling; } } void printHeap(Node h) { System.out.println("Binomial Heap: "); while (h != null) { System.out.print("B" + h.degree + ": "); printTree(h); System.out.println(); h = h.sibling; } } public static void main(String[] args) { BinomialHeap bh = new BinomialHeap(); Node hp = null; hp = bh.insert(hp, 10); hp = bh.insert(hp, 20); hp = bh.insert(hp, 30); hp = bh.insert(hp, 40); bh.printHeap(hp); } } 

 Binomial Heap: B2 : 10 20 30 40 

 class Node: def __init__(self, key): self.data = key self.degree = 0 self.child = self.parent = self.sibling = None def mergeBinomialTrees(b1, b2): if b1.data > b2.data: b1, b2 = b2, b1 b2.parent = b1 b2.sibling = b1.child b1.child = b2 b1.degree += 1 return b1 def unionBinomialHeap(h1, h2): if not h1: return h2 if not h2: return h1 dummy = Node(-1) # Dummy node to track merged heap tail = dummy curr1, curr2 = h1, h2 while curr1 and curr2: if curr1.degree <= curr2.degree: tail.sibling = curr1 curr1 = curr1.sibling else: tail.sibling = curr2 curr2 = curr2.sibling tail = tail.sibling tail.sibling = curr1 if curr1 else curr2 return dummy.sibling # Return merged heap without dummy node def adjustHeap(head): if not head: return None prev, curr, next = None, head, head.sibling while next: if curr.degree != next.degree or (next.sibling and next.sibling.degree == curr.degree): prev, curr = curr, next else: if curr.data <= next.data: curr.sibling = next.sibling curr = mergeBinomialTrees(curr, next) else: if prev: prev.sibling = next else: head = next curr = mergeBinomialTrees(next, curr) next = curr.sibling return head def insert(heap, key): temp = Node(key) return adjustHeap(unionBinomialHeap(heap, temp)) def printTree(h): while h: print(h.data, end=" ") printTree(h.child) h = h.sibling def printHeap(h): print("Binomial Heap:") while h: print("B" + str(h.degree) + ": ", end="") printTree(h) print() h = h.sibling # Testing the fixed binomial heap hp = None hp = insert(hp, 10) hp = insert(hp, 20) hp = insert(hp, 30) hp = insert(hp, 40) printHeap(hp) 

 Binomial Heap: B2: 10 20 30 40 

Extract-Min Operation in Binomial Heap

The extract-min operation removes the node with the smallest key from the binomial heap. The extract-min operation is performed as follows

 1. Find the node with the smallest key in the binomial heap. 2. Remove the node from the binomial heap. 3. Now, Let's Merge the children of the node with the binomial heap. 4. Adjust the binomial heap to maintain the heap property. 5. Return the new binomial heap. 

Code for Extract-Min Operation

Following is the implementation of extract-min operation in C, C++, Java and Python.

 #include <stdio.h> #include <stdlib.h> #include <limits.h> struct Node { int data, degree; struct Node *child, *sibling, *parent; }; struct Node *newNode(int key) { struct Node *temp = (struct Node *)malloc(sizeof(struct Node)); temp->data = key; temp->degree = 0; temp->child = temp->parent = temp->sibling = NULL; return temp; } struct Node *mergeBinomialTrees(struct Node *b1, struct Node *b2) { if (b1->data > b2->data) { struct Node *temp = b1; b1 = b2; b2 = temp; } b2->parent = b1; b2->sibling = b1->child; b1->child = b2; b1->degree++; return b1; } struct Node *unionBinomialHeap(struct Node *h1, struct Node *h2) { if (!h1) return h2; if (!h2) return h1; struct Node *newHeap = NULL, **pos = &newHeap; struct Node *curr1 = h1, *curr2 = h2; while (curr1 && curr2) { if (curr1->degree <= curr2->degree) { *pos = curr1; curr1 = curr1->sibling; } else { *pos = curr2; curr2 = curr2->sibling; } pos = &((*pos)->sibling); } *pos = (curr1) ? curr1 : curr2; return newHeap; } struct Node *adjustHeap(struct Node *head) { if (!head) return NULL; struct Node *prev = NULL, *curr = head, *next = head->sibling; while (next) { if (curr->degree != next->degree || (next->sibling && next->sibling->degree == curr->degree)) { prev = curr; curr = next; } else { if (curr->data <= next->data) { curr->sibling = next->sibling; curr = mergeBinomialTrees(curr, next); } else { if (!prev) head = next; else prev->sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr->sibling; } return head; } struct Node *insert(struct Node *heap, int key) { struct Node *temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } struct Node *getMin(struct Node *heap) { if (!heap) return NULL; struct Node *min = heap; struct Node *curr = heap->sibling; while (curr) { if (curr->data < min->data) min = curr; curr = curr->sibling; } return min; } struct Node *extractMin(struct Node *heap) { if (!heap) return NULL; struct Node *min = getMin(heap); struct Node *prev = NULL, *curr = heap; while (curr != min) { prev = curr; curr = curr->sibling; } if (prev) prev->sibling = min->sibling; else heap = min->sibling; struct Node *child = min->child; struct Node *newHeap = NULL; while (child) { struct Node *next = child->sibling; child->sibling = newHeap; child->parent = NULL; newHeap = child; child = next; } newHeap = adjustHeap(newHeap); return newHeap; } void printTree(struct Node *h) { while (h) { printf("%d ", h->data); printTree(h->child); h = h->sibling; } } void printHeap(struct Node *h) { printf("Binomial Heap: \n"); while (h) { printf("B%d: ", h->degree); printTree(h); printf("\n"); h = h->sibling; } } int main() { struct Node *hp = NULL; hp = insert(hp, 10); hp = insert(hp, 20); hp = insert(hp, 30); hp = insert(hp, 40); printHeap(hp); struct Node *min = getMin(hp); printf("Min: %d\n", min->data); hp = extractMin(hp); printHeap(hp); return 0; } 

 Binomial Heap: B0: 10 B1: 20 B2: 30 B3: 40 Min: 10 Binomial Heap: B1: 20 B2: 30 B3: 40 

 #include <iostream> #include <limits.h> using namespace std; struct Node { int data, degree; Node *child, *sibling, *parent; }; Node *newNode(int key) { Node *temp = new Node; temp->data = key; temp->degree = 0; temp->child = temp->parent = temp->sibling = NULL; return temp; } Node *mergeBinomialTrees(Node *b1, Node *b2) { if (b1->data > b2->data) { Node *temp = b1; b1 = b2; b2 = temp; } b2->parent = b1; b2->sibling = b1->child; b1->child = b2; b1->degree++; return b1; } Node *unionBinomialHeap(Node *h1, Node *h2) { if (!h1) return h2; if (!h2) return h1; Node *newHeap = NULL, **pos = &newHeap; Node *curr1 = h1, *curr2 = h2; while (curr1 && curr2) { if (curr1->degree <= curr2->degree) { *pos = curr1; curr1 = curr1->sibling; } else { *pos = curr2; curr2 = curr2->sibling; } pos = &((*pos)->sibling); } *pos = (curr1) ? curr1 : curr2; return newHeap; } Node *adjustHeap(Node *head) { if (!head) return NULL; Node *prev = NULL, *curr = head, *next = head->sibling; while (next) { if (curr->degree != next->degree || (next->sibling && next->sibling->degree == curr->degree)) { prev = curr; curr = next; } else { if (curr->data <= next->data) { curr->sibling = next->sibling; curr = mergeBinomialTrees(curr, next); } else { if (!prev) head = next; else prev->sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr->sibling; } return head; } Node *insert(Node *heap, int key) { Node *temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } Node *getMin(Node *heap) { if (!heap) return NULL; Node *min = heap; Node *curr = heap->sibling; while (curr) { if (curr->data < min->data) min = curr; curr = curr->sibling; } return min; } Node *extractMin(Node *heap) { if (!heap) return NULL; Node *min = getMin(heap); Node *prev = NULL, *curr = heap; while (curr != min) { prev = curr; curr = curr->sibling; } if (prev) prev->sibling = min->sibling; else heap = min->sibling; Node *child = min->child; Node *newHeap = NULL; while (child) { Node *next = child->sibling; child->sibling = newHeap; child->parent = NULL; newHeap = child; child = next; } newHeap = adjustHeap(newHeap); return newHeap; } void printTree(Node *h) { while (h) { cout << h->data << " "; printTree(h->child); h = h->sibling; } } void printHeap(Node *h) { cout << "Binomial Heap: " << endl; while (h) { cout << "B" << h->degree << ": "; printTree(h); cout << endl; h = h->sibling; } } int main() { Node *hp = NULL; hp = insert(hp, 10); hp = insert(hp, 20); hp = insert(hp, 30); hp = insert(hp, 40); printHeap(hp); Node *min = getMin(hp); cout << "Min: " << min->data << endl; hp = extractMin(hp); printHeap(hp); return 0; } 

 Binomial Heap: B0: 10 B1: 20 B2: 30 B3: 40 Min: 10 Binomial Heap: B1: 20 B2: 30 B3: 40 

 import java.util.*; class Node { int data, degree; Node child, parent, sibling; } public class BinomialHeap { Node newNode(int key) { Node temp = new Node(); temp.data = key; temp.degree = 0; temp.child = temp.parent = temp.sibling = null; return temp; } Node mergeBinomialTrees(Node b1, Node b2) { if (b1.data > b2.data) { Node temp = b1; b1 = b2; b2 = temp; } b2.parent = b1; b2.sibling = b1.child; b1.child = b2; b1.degree++; return b1; } Node unionBinomialHeap(Node h1, Node h2) { if (h1 == null) return h2; if (h2 == null) return h1; Node dummy = new Node(); Node tail = dummy; Node curr1 = h1, curr2 = h2; while (curr1 != null && curr2 != null) { if (curr1.degree <= curr2.degree) { tail.sibling = curr1; curr1 = curr1.sibling; } else { tail.sibling = curr2; curr2 = curr2.sibling; } tail = tail.sibling; } tail.sibling = (curr1 != null) ? curr1 : curr2; return dummy.sibling; } Node adjustHeap(Node head) { if (head == null) return null; Node prev = null, curr = head, next = head.sibling; while (next != null) { if (curr.degree != next.degree || (next.sibling != null && next.sibling.degree == curr.degree)) { prev = curr; curr = next; } else { if (curr.data <= next.data) { curr.sibling = next.sibling; curr = mergeBinomialTrees(curr, next); } else { if (prev == null) head = next; else prev.sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr.sibling; } return head; } Node insert(Node heap, int key) { Node temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } Node getMin(Node heap) { if (heap == null) return null; Node min = heap; Node curr = heap.sibling; while (curr != null) { if (curr.data < min.data) min = curr; curr = curr.sibling; } return min; } Node extractMin(Node heap) { if (heap == null) return null; Node min = getMin(heap); Node prev = null, curr = heap; while (curr != min) { prev = curr; curr = curr.sibling; } if (prev != null) prev.sibling = min.sibling; else heap = min.sibling; // Reverse child list Node child = min.child; Node newHeap = null; while (child != null) { Node next = child.sibling; child.sibling = newHeap; child.parent = null; newHeap = child; child = next; } return adjustHeap(unionBinomialHeap(heap, newHeap)); } void printTree(Node h) { while (h != null) { System.out.print(h.data + " "); printTree(h.child); h = h.sibling; } } void printHeap(Node h) { System.out.println("Binomial Heap: "); while (h != null) { System.out.print("B" + h.degree + ": "); printTree(h); System.out.println(); h = h.sibling; } } public static void main(String[] args) { BinomialHeap bh = new BinomialHeap(); Node hp = null; hp = bh.insert(hp, 10); hp = bh.insert(hp, 20); hp = bh.insert(hp, 30); hp = bh.insert(hp, 40); bh.printHeap(hp); Node min = bh.getMin(hp); System.out.println("Min: " + min.data); hp = bh.extractMin(hp); bh.printHeap(hp); } } 

 Binomial Heap: B0: 10 B1: 20 B2: 30 B3: 40 Min: 10 Binomial Heap: B1: 20 B2: 30 B3: 40 

 class Node: def __init__(self, key): self.data = key self.degree = 0 self.child = self.parent = self.sibling = None def mergeBinomialTrees(b1, b2): if b1.data > b2.data: temp = b1 b1 = b2 b2 = temp b2.parent = b1 b2.sibling = b1.child b1.child = b2 b1.degree += 1 return b1 def unionBinomialHeap(h1, h2): if not h1: return h2 if not h2: return h1 newHeap = None if h1.degree <= h2.degree: newHeap = h1 h1 = h1.sibling else: newHeap = h2 h2 = h2.sibling pos = newHeap while h1 and h2: if h1.degree <= h2.degree: pos.sibling = h1 h1 = h1.sibling else: pos.sibling = h2 h2 = h2.sibling pos = pos.sibling if h1: pos.sibling = h1 else: pos.sibling = h2 return newHeap def adjustHeap(head): if not head: return None prev = None curr = head next = head.sibling while next: if curr.degree != next.degree or (next.sibling and next.sibling.degree == curr.degree): prev = curr curr = next else: if curr.data <= next.data: curr.sibling = next.sibling curr = mergeBinomialTrees(curr, next) else: if not prev: head = next else: prev.sibling = next curr = mergeBinomialTrees(next, curr) next = curr.sibling return head def insert(heap, key): temp = Node(key) return adjustHeap(unionBinomialHeap(heap, temp)) def getMin(heap): if not heap: return None min = heap curr = heap.sibling while curr: if curr.data < min.data: min = curr curr = curr.sibling return min def extractMin(heap): if not heap: return None min = getMin(heap) prev = None curr = heap while curr != min: prev = curr curr = curr.sibling if prev: prev.sibling = min.sibling else: heap = min.sibling child = min.child newHeap = None while child: next = child.sibling child.sibling = newHeap child.parent = None newHeap = child child = next newHeap = adjustHeap(newHeap) return newHeap def printTree(h): while h: print(h.data, end=" ") printTree(h.child) h = h.sibling def printHeap(h): print("Binomial Heap: ") while h: print("B" + str(h.degree) + ": ", end="") printTree(h) print() h = h.sibling hp = None hp = insert(hp, 10) hp = insert(hp, 20) hp = insert(hp, 30) hp = insert(hp, 40) printHeap(hp) min = getMin(hp) print("Min: " + str(min.data)) hp = extractMin(hp) printHeap(hp) 

 Binomial Heap: B0: 10 B1: 20 B2: 30 B3: 40 Min: 10 Binomial Heap: B1: 20 B2: 30 B3: 40 

Decrease-Key Operation in Binomial Heap

Decrease-key is a important operation in the binomial heap. It is used to decrease the value of a key in the binomial heap. The decrease-key operation is performed as follows

Algorithm for Decrease-Key Operation

Follow the steps below to decrease-key.

 1. Decrease the value of the key to a new value. 2. If the new value is greater than the parent of the node, then return. 3. If the new value is less than the parent of the node, then swap the values of the node and its parent. 4. Repeat the above step until the node reaches the root or the parent of the node is less than the node. 

Code for Decrease-Key Operation in Binomial Heap

Following is the implementation of decrease-key operation in C, C++, Java and Python.

 #include <stdio.h> #include <stdlib.h> #include <limits.h> struct Node { int data, degree; struct Node *child, *sibling, *parent; }; struct Node *newNode(int key) { struct Node *temp = (struct Node *)malloc(sizeof(struct Node)); temp->data = key; temp->degree = 0; temp->child = temp->parent = temp->sibling = NULL; return temp; } struct Node *mergeBinomialTrees(struct Node *b1, struct Node *b2) { if (b1->data > b2->data) { struct Node *temp = b1; b1 = b2; b2 = temp; } b2->parent = b1; b2->sibling = b1->child; b1->child = b2; b1->degree++; return b1; } struct Node *unionBinomialHeap(struct Node *h1, struct Node *h2) { if (!h1) return h2; if (!h2) return h1; struct Node *newHeap = NULL, **pos = &newHeap; struct Node *curr1 = h1, *curr2 = h2; while (curr1 && curr2) { if (curr1->degree <= curr2->degree) { *pos = curr1; curr1 = curr1->sibling; } else { *pos = curr2; curr2 = curr2->sibling; } pos = &((*pos)->sibling); } *pos = (curr1) ? curr1 : curr2; return newHeap; } struct Node *adjustHeap(struct Node *head) { if (!head) return NULL; struct Node *prev = NULL, *curr = head, *next = head->sibling; while (next) { if (curr->degree != next->degree || (next->sibling && next->sibling->degree == curr->degree)) { prev = curr; curr = next; } else { if (curr->data <= next->data) { curr->sibling = next->sibling; curr = mergeBinomialTrees(curr, next); } else { if (!prev) head = next; else prev->sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr->sibling; } return head; } struct Node *insert(struct Node *heap, int key) { struct Node *temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } struct Node *getMin(struct Node *heap) { if (!heap) return NULL; struct Node *min = heap; struct Node *curr = heap->sibling; while (curr) { if (curr->data < min->data) min = curr; curr = curr->sibling; } return min; } struct Node *extractMin(struct Node *heap) { if (!heap) return NULL; struct Node *min = getMin(heap); struct Node *prev = NULL, *curr = heap; while (curr != min) { prev = curr; curr = curr->sibling; } if (prev) prev->sibling = min->sibling; else heap = min->sibling; struct Node *child = min->child; struct Node *newHeap = NULL; while (child) { struct Node *next = child->sibling; child->sibling = newHeap; child->parent = NULL; newHeap = child; child = next; } newHeap = adjustHeap(newHeap); return newHeap; } void decreaseKey(struct Node *heap, struct Node *node, int key) { if (!heap || !node) return; if (key > node->data) return; node->data = key; struct Node *parent = node->parent; while (parent && node->data < parent->data) { int temp = node->data; node->data = parent->data; parent->data = temp; node = parent; parent = node->parent; } } void printTree(struct Node *h) { while (h) { printf("%d ", h->data); printTree(h->child); h = h->sibling; } } void printHeap(struct Node *h) { while (h) { printf("B%d: ", h->degree); printTree(h); printf("\n"); h = h->sibling; } } int main() { struct Node *hp = NULL; hp = insert(hp, 10); hp = insert(hp, 20); hp = insert(hp, 30); hp = insert(hp, 40); printf("Binomial Heap: \n"); printHeap(hp); struct Node *min = getMin(hp); printf("Min: %d\n", min->data); decreaseKey(hp, hp->sibling, 5); printf("Binomial Heap after Decrease-Key operation\n"); printHeap(hp); return 0; } 

 Binomial Heap: B2: 10 30 40 20 Min: 10 Binomial Heap after Decrease-Key operation B2: 10 30 40 20 

 #include <iostream> #include <limits.h> using namespace std; struct Node { int data, degree; Node *child, *sibling, *parent; }; Node *newNode(int key) { Node *temp = new Node; temp->data = key; temp->degree = 0; temp->child = temp->parent = temp->sibling = NULL; return temp; } Node *mergeBinomialTrees(Node *b1, Node *b2) { if (b1->data > b2->data) { Node *temp = b1; b1 = b2; b2 = temp; } b2->parent = b1; b2->sibling = b1->child; b1->child = b2; b1->degree++; return b1; } Node *unionBinomialHeap(Node *h1, Node *h2) { if (!h1) return h2; if (!h2) return h1; Node *newHeap = NULL, **pos = &newHeap; Node *curr1 = h1, *curr2 = h2; while (curr1 && curr2) { if (curr1->degree <= curr2->degree) { *pos = curr1; curr1 = curr1->sibling; } else { *pos = curr2; curr2 = curr2->sibling; } pos = &((*pos)->sibling); } *pos = (curr1) ? curr1 : curr2; return newHeap; } Node *adjustHeap(Node *head) { if (!head) return NULL; Node *prev = NULL, *curr = head, *next = head->sibling; while (next) { if (curr->degree != next->degree || (next->sibling && next->sibling->degree == curr->degree)) { prev = curr; curr = next; } else { if (curr->data <= next->data) { curr->sibling = next->sibling; curr = mergeBinomialTrees(curr, next); } else { if (!prev) head = next; else prev->sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr->sibling; } return head; } Node *insert(Node *heap, int key) { Node *temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } Node *getMin(Node *heap) { if (!heap) return NULL; Node *min = heap; Node *curr = heap->sibling; while (curr) { if (curr->data < min->data) min = curr; curr = curr->sibling; } return min; } Node *extractMin(Node *heap) { if (!heap) return NULL; Node *min = getMin(heap); Node *prev = NULL, *curr = heap; while (curr != min) { prev = curr; curr = curr->sibling; } if (prev) prev->sibling = min->sibling; else heap = min->sibling; Node *child = min->child; Node *newHeap = NULL; while (child) { Node *next = child->sibling; child->sibling = newHeap; child->parent = NULL; newHeap = child; child = next; } newHeap = adjustHeap(newHeap); return newHeap; } void decreaseKey(Node *heap, Node *node, int key) { if (!heap || !node) return; if (key > node->data) return; node->data = key; Node *parent = node->parent; while (parent && node->data < parent->data) { int temp = node->data; node->data = parent->data; parent->data = temp; node = parent; parent = node->parent; } } void printTree(Node *h) { while (h) { cout << h->data << " "; printTree(h->child); h = h->sibling; } } void printHeap(Node *h) { while (h) { cout << "B" << h->degree << ": "; printTree(h); cout << endl; h = h->sibling; } } int main() { Node *hp = NULL; hp = insert(hp, 10); hp = insert(hp, 20); hp = insert(hp, 30); hp = insert(hp, 40); cout << "Binomial Heap:" << endl; printHeap(hp); Node *min = getMin(hp); cout << "Min: " << min->data << endl; decreaseKey(hp, hp->sibling, 5); cout << "Binomial Heap after Decrease-Key operation" << endl; printHeap(hp); return 0; } 

 Binomial Heap: B2: 10 30 40 20 Min: 10 Binomial Heap after Decrease-Key operation B2: 10 30 40 20 

 import java.util.*; class Node { int data, degree; Node child, parent, sibling; } public class BinomialHeap { Node newNode(int key) { Node temp = new Node(); temp.data = key; temp.degree = 0; temp.child = temp.parent = temp.sibling = null; return temp; } Node mergeBinomialTrees(Node b1, Node b2) { if (b1.data > b2.data) { Node temp = b1; b1 = b2; b2 = temp; } b2.parent = b1; b2.sibling = b1.child; b1.child = b2; b1.degree++; return b1; } Node unionBinomialHeap(Node h1, Node h2) { if (h1 == null) return h2; if (h2 == null) return h1; Node newHeap = null, tail = null; Node curr1 = h1, curr2 = h2; // Merging two heaps by linking nodes in increasing order of degree while (curr1 != null && curr2 != null) { Node smaller; if (curr1.degree <= curr2.degree) { smaller = curr1; curr1 = curr1.sibling; } else { smaller = curr2; curr2 = curr2.sibling; } if (newHeap == null) { newHeap = smaller; tail = newHeap; } else { tail.sibling = smaller; tail = tail.sibling; } } if (curr1 != null) tail.sibling = curr1; if (curr2 != null) tail.sibling = curr2; return newHeap; } Node adjustHeap(Node head) { if (head == null) return null; Node prev = null, curr = head, next = head.sibling; while (next != null) { if (curr.degree != next.degree || (next.sibling != null && next.sibling.degree == curr.degree)) { prev = curr; curr = next; } else { if (curr.data <= next.data) { curr.sibling = next.sibling; curr = mergeBinomialTrees(curr, next); } else { if (prev == null) head = next; else prev.sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr.sibling; } return head; } Node insert(Node heap, int key) { Node temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } Node getMin(Node heap) { if (heap == null) return null; Node min = heap; Node curr = heap.sibling; while (curr != null) { if (curr.data < min.data) min = curr; curr = curr.sibling; } return min; } Node extractMin(Node heap) { if (heap == null) return null; Node min = getMin(heap); Node prev = null, curr = heap; while (curr != min) { prev = curr; curr = curr.sibling; } if (prev != null) prev.sibling = min.sibling; else heap = min.sibling; Node child = min.child; Node newHeap = null; while (child != null) { Node next = child.sibling; child.sibling = newHeap; child.parent = null; newHeap = child; child = next; } return adjustHeap(unionBinomialHeap(heap, newHeap)); } void decreaseKey(Node heap, Node node, int key) { if (heap == null || node == null) return; if (key > node.data) return; node.data = key; Node parent = node.parent; while (parent != null && node.data < parent.data) { int temp = node.data; node.data = parent.data; parent.data = temp; node = parent; parent = node.parent; } } void printTree(Node h) { while (h != null) { System.out.print(h.data + " "); printTree(h.child); h = h.sibling; } } void printHeap(Node h) { while (h != null) { System.out.print("B" + h.degree + ": "); printTree(h); System.out.println(); h = h.sibling; } } public static void main(String[] args) { BinomialHeap bh = new BinomialHeap(); Node hp = null; hp = bh.insert(hp, 10); hp = bh.insert(hp, 20); hp = bh.insert(hp, 30); hp = bh.insert(hp, 40); System.out.println("Binomial Heap:"); bh.printHeap(hp); Node min = bh.getMin(hp); System.out.println("Min: " + min.data); // Find node with value 30 and decrease its key to 5 Node nodeToDecrease = hp.child != null ? hp.child.sibling : null; // Assuming 30 is at this position if (nodeToDecrease != null) { bh.decreaseKey(hp, nodeToDecrease, 5); } System.out.println("Binomial Heap after Decrease-Key operation:"); bh.printHeap(hp); } } 

 Binomial Heap: B2: 10 30 40 20 Min: 10 Binomial Heap after Decrease-Key operation: B2: 5 30 40 10 

 class Node: def __init__(self, key): self.data = key self.degree = 0 self.child = self.parent = self.sibling = None def mergeBinomialTrees(b1, b2): if b1.data > b2.data: b1, b2 = b2, b1 # Ensure b1 is the root b2.parent = b1 b2.sibling = b1.child b1.child = b2 b1.degree += 1 return b1 def unionBinomialHeap(h1, h2): if not h1: return h2 if not h2: return h1 head, tail = None, None while h1 and h2: if h1.degree <= h2.degree: node = h1 h1 = h1.sibling else: node = h2 h2 = h2.sibling if not head: head = node tail = node else: tail.sibling = node tail = node tail.sibling = h1 if h1 else h2 return head def adjustHeap(head): if not head: return None prev, curr, next = None, head, head.sibling while next: if curr.degree != next.degree or (next.sibling and next.sibling.degree == curr.degree): prev = curr curr = next else: if curr.data <= next.data: curr.sibling = next.sibling curr = mergeBinomialTrees(curr, next) else: if prev: prev.sibling = next else: head = next curr = mergeBinomialTrees(next, curr) next = curr.sibling return head def insert(heap, key): temp = Node(key) return adjustHeap(unionBinomialHeap(heap, temp)) def getMin(heap): if not heap: return None minNode = heap curr = heap.sibling while curr: if curr.data < minNode.data: minNode = curr curr = curr.sibling return minNode def extractMin(heap): if not heap: return None minNode = getMin(heap) prev, curr = None, heap while curr != minNode: prev = curr curr = curr.sibling if prev: prev.sibling = minNode.sibling else: heap = minNode.sibling child = minNode.child newHeap = None while child: nextChild = child.sibling child.sibling = newHeap child.parent = None newHeap = child child = nextChild return adjustHeap(unionBinomialHeap(heap, newHeap)) def decreaseKey(heap, node, key): if not node or key > node.data: return node.data = key parent = node.parent while parent and node.data < parent.data: node.data, parent.data = parent.data, node.data node = parent parent = node.parent def printTree(h): while h: print(h.data, end=" ") printTree(h.child) h = h.sibling def printHeap(h): while h: print(f"B{h.degree}: ", end="") printTree(h) print() h = h.sibling # Testing the heap hp = None hp = insert(hp, 10) hp = insert(hp, 20) hp = insert(hp, 30) hp = insert(hp, 40) print("Binomial Heap:") printHeap(hp) minNode = getMin(hp) print("Min:", minNode.data) if hp.child: decreaseKey(hp, hp.child, 5) print("Binomial Heap after Decrease-Key operation:") printHeap(hp) 

 Binomial Heap: B2: 10 30 40 20 Min: 10 Binomial Heap after Decrease-Key operation: B2: 5 10 40 20 

Delete Operation in Binomial Heap

Delete operation is used for deleting a key from a binomial heap.

Algorithm for Delete Operation

 1. Decrease the key value to minus infinity. 2. Now extract the minimum value from the heap. 

Code for Delete Operation in Binomial Heap

Following is the implementation of delete operation in C, C++, Java and Python.

 #include <stdio.h> #include <stdlib.h> #include <limits.h> struct Node { int data, degree; struct Node *child, *sibling, *parent; }; struct Node *newNode(int key) { struct Node *temp = (struct Node *)malloc(sizeof(struct Node)); temp->data = key; temp->degree = 0; temp->child = temp->parent = temp->sibling = NULL; return temp; } struct Node *mergeBinomialTrees(struct Node *b1, struct Node *b2) { if (b1->data > b2->data) { struct Node *temp = b1; b1 = b2; b2 = temp; } b2->parent = b1; b2->sibling = b1->child; b1->child = b2; b1->degree++; return b1; } struct Node *unionBinomialHeap(struct Node *h1, struct Node *h2) { if (!h1) return h2; if (!h2) return h1; struct Node *newHeap = NULL, **pos = &newHeap; struct Node *curr1 = h1, *curr2 = h2; while (curr1 && curr2) { if (curr1->degree <= curr2->degree) { *pos = curr1; curr1 = curr1->sibling; } else { *pos = curr2; curr2 = curr2->sibling; } pos = &((*pos)->sibling); } *pos = (curr1) ? curr1 : curr2; return newHeap; } struct Node *adjustHeap(struct Node *head) { if (!head) return NULL; struct Node *prev = NULL, *curr = head, *next = head->sibling; while (next) { if (curr->degree != next->degree || (next->sibling && next->sibling->degree == curr->degree)) { prev = curr; curr = next; } else { if (curr->data <= next->data) { curr->sibling = next->sibling; curr = mergeBinomialTrees(curr, next); } else { if (!prev) head = next; else prev->sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr->sibling; } return head; } struct Node *insert(struct Node *heap, int key) { struct Node *temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } struct Node *getMin(struct Node *heap) { if (!heap) return NULL; struct Node *min = heap; struct Node *curr = heap->sibling; while (curr) { if (curr->data < min->data) min = curr; curr = curr->sibling; } return min; } struct Node *extractMin(struct Node *heap) { if (!heap) return NULL; struct Node *min = getMin(heap); struct Node *prev = NULL, *curr = heap; while (curr != min) { prev = curr; curr = curr->sibling; } if (prev) prev->sibling = min->sibling; else heap = min->sibling; struct Node *child = min->child; struct Node *newHeap = NULL; while (child) { struct Node *next = child->sibling; child->sibling = newHeap; child->parent = NULL; newHeap = child; child = next; } newHeap = adjustHeap(newHeap); return newHeap; } void deleteKey(struct Node **heap, struct Node *node) { if (!*heap || !node) return; node->data = INT_MIN; struct Node *parent = node->parent; while (parent && node->data < parent->data) { int temp = node->data; node->data = parent->data; parent->data = temp; node = parent; parent = node->parent; } *heap = extractMin(*heap); } void printTree(struct Node *h) { while (h) { printf("%d ", h->data); printTree(h->child); h = h->sibling; } } void printHeap(struct Node *h) { printf("Binomial Heap: \n"); while (h) { printf("B%d: ", h->degree); printTree(h); printf("\n"); h = h->sibling; } } int main() { struct Node *hp = NULL; hp = insert(hp, 10); hp = insert(hp, 20); hp = insert(hp, 30); hp = insert(hp, 40); printHeap(hp); struct Node *min = getMin(hp); printf("Min: %d\n", min->data); deleteKey(&hp, hp->sibling); printf("Binomial Heap after Delete operation\n"); printHeap(hp); return 0; } 

 Binomial Heap: B0: 10 B1: 20 B2: 30 B3: 40 Min: 10 Binomial Heap after Delete operation B0: 10 B1: 30 B2: 40 

 #include <iostream> #include <limits.h> using namespace std; struct Node { int data, degree; Node *child, *sibling, *parent; }; Node *newNode(int key) { Node *temp = new Node; temp->data = key; temp->degree = 0; temp->child = temp->parent = temp->sibling = NULL; return temp; } Node *mergeBinomialTrees(Node *b1, Node *b2) { if (b1->data > b2->data) { Node *temp = b1; b1 = b2; b2 = temp; } b2->parent = b1; b2->sibling = b1->child; b1->child = b2; b1->degree++; return b1; } Node *unionBinomialHeap(Node *h1, Node *h2) { if (!h1) return h2; if (!h2) return h1; Node *newHeap = NULL, **pos = &newHeap; Node *curr1 = h1, *curr2 = h2; while (curr1 && curr2) { if (curr1->degree <= curr2->degree) { *pos = curr1; curr1 = curr1->sibling; } else { *pos = curr2; curr2 = curr2->sibling; } pos = &((*pos)->sibling); } *pos = (curr1) ? curr1 : curr2; return newHeap; } Node *adjustHeap(Node *head) { if (!head) return NULL; Node *prev = NULL, *curr = head, *next = head->sibling; while (next) { if (curr->degree != next->degree || (next->sibling && next->sibling->degree == curr->degree)) { prev = curr; curr = next; } else { if (curr->data <= next->data) { curr->sibling = next->sibling; curr = mergeBinomialTrees(curr, next); } else { if (!prev) head = next; else prev->sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr->sibling; } return head; } Node *insert(Node *heap, int key) { Node *temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } Node *getMin(Node *heap) { if (!heap) return NULL; Node *min = heap; Node *curr = heap->sibling; while (curr) { if (curr->data < min->data) min = curr; curr = curr->sibling; } return min; } Node *extractMin(Node *heap) { if (!heap) return NULL; Node *min = getMin(heap); Node *prev = NULL, *curr = heap; while (curr != min) { prev = curr; curr = curr->sibling; } if (prev) prev->sibling = min->sibling; else heap = min->sibling; Node *child = min->child; Node *newHeap = NULL; while (child) { Node *next = child->sibling; child->sibling = newHeap; child->parent = NULL; newHeap = child; child = next; } newHeap = adjustHeap(newHeap); return newHeap; } void deleteKey(Node *heap, Node *node) { if (!heap || !node) return; node->data = INT_MIN; Node *parent = node->parent; while (parent && node->data < parent->data) { int temp = node->data; node->data = parent->data; parent->data = temp; node = parent; parent = node->parent; } extractMin(heap); } void printTree(Node *h) { while (h) { cout << h->data << " "; printTree(h->child); h = h->sibling; } } void printHeap(Node *h) { cout << "Binomial Heap: " << endl; while (h) { cout << "B" << h->degree << ": "; printTree(h); cout << endl; h = h->sibling; } } int main() { Node *hp = NULL; hp = insert(hp, 10); hp = insert(hp, 20); hp = insert(hp, 30); hp = insert(hp, 40); printHeap(hp); Node *min = getMin(hp); cout << "Min: " << min->data << endl; deleteKey(hp, hp->sibling); cout << "Binomial Heap after Delete operation" << endl; printHeap(hp); return 0; } 

 Binomial Heap: B0: 10 B1: 20 B2: 30 B3: 40 Min: 10 Binomial Heap after Delete operation B0: 10 B1: 30 B2: 40 

 import java.util.*; class Node { int data, degree; Node child, parent, sibling; } public class BinomialHeap { Node newNode(int key) { Node temp = new Node(); temp.data = key; temp.degree = 0; temp.child = temp.parent = temp.sibling = null; return temp; } Node mergeBinomialTrees(Node b1, Node b2) { if (b1.data > b2.data) { Node temp = b1; b1 = b2; b2 = temp; } b2.parent = b1; b2.sibling = b1.child; b1.child = b2; b1.degree++; return b1; } Node unionBinomialHeap(Node h1, Node h2) { if (h1 == null) return h2; if (h2 == null) return h1; Node newHeap = null, pos = newHeap; Node curr1 = h1, curr2 = h2; while (curr1 != null && curr2 != null) { if (curr1.degree <= curr2.degree) { if (newHeap == null) { newHeap = curr1; pos = curr1; } else { pos.sibling = curr1; pos = curr1; } curr1 = curr1.sibling; } else { if (newHeap == null) { newHeap = curr2; pos = curr2; } else { pos.sibling = curr2; pos = curr2; } curr2 = curr2.sibling; } } if (curr1 != null) pos.sibling = curr1; if (curr2 != null) pos.sibling = curr2; return newHeap; } Node adjustHeap(Node head) { if (head == null) return null; Node prev = null, curr = head, next = head.sibling; while (next != null) { if (curr.degree != next.degree || (next.sibling != null && next.sibling.degree == curr.degree)) { prev = curr; curr = next; } else { if (curr.data <= next.data) { curr.sibling = next.sibling; curr = mergeBinomialTrees(curr, next); } else { if (prev == null) head = next; else prev.sibling = next; curr = mergeBinomialTrees(next, curr); } } next = curr.sibling; } return head; } Node insert(Node heap, int key) { Node temp = newNode(key); return adjustHeap(unionBinomialHeap(heap, temp)); } Node getMin(Node heap) { if (heap == null) return null; Node min = heap; Node curr = heap.sibling; while (curr != null) { if (curr.data < min.data) min = curr; curr = curr.sibling; } return min; } Node extractMin(Node heap) { if (heap == null) return null; Node min = getMin(heap); Node prev = null, curr = heap; while (curr != min) { prev = curr; curr = curr.sibling; } if (prev != null) prev.sibling = min.sibling; else heap = min.sibling; Node child = min.child; Node newHeap = null; while (child != null) { Node next = child.sibling; child.sibling = newHeap; child.parent = null; newHeap = child; child = next; } newHeap = adjustHeap(newHeap); return newHeap; } void deleteKey(Node heap, Node node) { if (heap == null || node == null) return; node.data = Integer.MIN_VALUE; Node parent = node.parent; while (parent != null && node.data < parent.data) { int temp = node.data; node.data = parent.data; parent.data = temp; node = parent; parent = node.parent; } extractMin(heap); } void printTree(Node h) { while (h != null) { System.out.print(h.data + " "); printTree(h.child); h = h.sibling; } } void printHeap(Node h) { System.out.println("Binomial Heap: "); while (h != null) { System.out.print("B" + h.degree + ": "); printTree(h); System.out.println(); h = h.sibling; } } public static void main(String[] args) { BinomialHeap bh = new BinomialHeap(); Node hp = null; hp = bh.insert(hp, 10); hp = bh.insert(hp, 20); hp = bh.insert(hp, 30); hp = bh.insert(hp, 40); bh.printHeap(hp); Node min = bh.getMin(hp); System.out.println("Min: " + min.data); bh.deleteKey(hp, hp.child); System.out.println("Binomial Heap after Delete operation"); bh.printHeap(hp); } } 

 Binomial Heap: B0: 10 B1: 20 B2: 30 B3: 40 Min: 10 Binomial Heap after Delete operation B0: 10 B1: 30 B2: 40 

 class Node: def __init__(self, key): self.data = key self.degree = 0 self.child = self.parent = self.sibling = None def mergeBinomialTrees(b1, b2): if b1.data > b2.data: b1, b2 = b2, b1 # Ensure b1 is the root b2.parent = b1 b2.sibling = b1.child b1.child = b2 b1.degree += 1 return b1 def unionBinomialHeap(h1, h2): if not h1: return h2 if not h2: return h1 head, tail = None, None while h1 and h2: if h1.degree <= h2.degree: node = h1 h1 = h1.sibling else: node = h2 h2 = h2.sibling if not head: head = node tail = node else: tail.sibling = node tail = node tail.sibling = h1 if h1 else h2 return head def adjustHeap(head): if not head: return None prev, curr, next = None, head, head.sibling while next: if curr.degree != next.degree or (next.sibling and next.sibling.degree == curr.degree): prev = curr curr = next else: if curr.data <= next.data: curr.sibling = next.sibling curr = mergeBinomialTrees(curr, next) else: if prev: prev.sibling = next else: head = next curr = mergeBinomialTrees(next, curr) next = curr.sibling return head def insert(heap, key): temp = Node(key) return adjustHeap(unionBinomialHeap(heap, temp)) def getMin(heap): if not heap: return None minNode = heap curr = heap.sibling while curr: if curr.data < minNode.data: minNode = curr curr = curr.sibling return minNode def extractMin(heap): if not heap: return None minNode = getMin(heap) prev, curr = None, heap while curr != minNode: prev = curr curr = curr.sibling if prev: prev.sibling = minNode.sibling else: heap = minNode.sibling child = minNode.child newHeap = None while child: nextChild = child.sibling child.sibling = newHeap child.parent = None newHeap = child child = nextChild return adjustHeap(unionBinomialHeap(heap, newHeap)) def decreaseKey(heap, node, key): if not node or key > node.data: return node.data = key parent = node.parent while parent and node.data < parent.data: node.data, parent.data = parent.data, node.data node = parent parent = node.parent def printTree(h): while h: print(h.data, end=" ") printTree(h.child) h = h.sibling def printHeap(h): while h: print(f"B{h.degree}: ", end="") printTree(h) print() h = h.sibling # Testing the heap def deleteKey(heap, node): if not heap or not node: return node.data = float('-inf') parent = node.parent while parent and node.data < parent.data: node.data, parent.data = parent.data, node.data node = parent parent = node.parent extractMin(heap) hp = None hp = insert(hp, 10) hp = insert(hp, 20) hp = insert(hp, 30) hp = insert(hp, 40) printHeap(hp) min_node = getMin(hp) print("Min:", min_node.data) deleteKey(hp, hp.child) print("Binomial Heap after Delete operation:") printHeap(hp) 

 Binomial Heap: B0: 10 B1: 20 B2: 30 B3: 40 Min: 10 Binomial Heap after Delete operation B0: 10 B1: 30 B2: 40 

Time Complexity of Binomial Heap

Following are the time complexities of the Binomial Heap

• Insertion: O(log n)
• Deletion: O(log n)
• Decrease-Key: O(log n)
• Extract-Min: O(log n)
• Get-Min: O(1)

Applications of Binomial Heap

Binomial heaps are used in plenty of applications. Some of them are listed below

• Used in implementing priority queues.
• Dijkstra's shortest path algorithm.
• Prim's minimum spanning tree algorithm.
• Used in garbage collection.

Conclusion

In this tutorial, we have learned about Binomial Heap, its operations, and its implementation in C, C++, Java, and Python. We also discussed the time complexity of the Binomial Heap and its applications.