Lattice Path in Discrete Mathematics

Lattice paths are all about moving along a grid. If we think about standing on a grid of squares, where we can only move in two directions: to the right or upward. A lattice path is simply the shortest route from one point on that grid to another, only taking those two allowed moves.

In discrete mathematics, lattice paths are used to solve problems related to counting the number of ways we can reach a certain point on a grid. Read this chapter to learn the basics of lattice paths and how they work.

What is a Lattice Path?

Before we understand it mathematically, let us define what a lattice is. A lattice is nothing but a grid of points, where each point has integer coordinates. Imagine the grid lines on graph paper, where each intersection is a point with integer x and y coordinates.

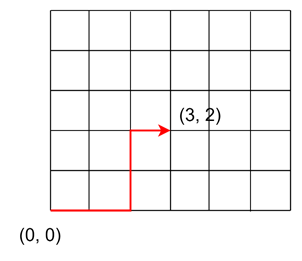
The above grid is a lattice and the red path could be the lattice path. A lattice path is the shortest possible route between two points on this grid.

Here, each step either moves to the right or moves the upward. We are not allowed to move diagonally, and we cannot go backwards. So, if we start at (0, 0) and want to reach (3, 2), for example, we have to make exactly 3 steps to the right and 2 steps up, no matter the order in which we take those steps.

Example of a Lattice Path

Let us see an example to make it clearer. Say we want to move from the point (0, 0) to the point (3, 2). One possible path could be −

• Right (R), Right (R), Up (U), Up (U), Right (R) (as shown in the above figure)

This is written as “RRUUR.” But that is just one way to do it. You could also mix up the steps, like this:

• UURRR (first move up twice, then right three times)

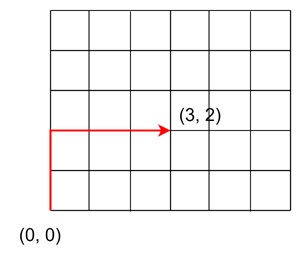
Or you could try this,

• RURRU (right, up, right, right, up)

Each of these sequences represents a different lattice path, but they all start at (0, 0) and end at (3, 2). The important thing is that every path takes exactly five steps: three right and two up.

Counting Lattice Paths

Now, the question comes, how do we know how many lattice paths exist between two points? Specifically, let us understand the example of moving from (0, 0) to (3, 2). Each valid path has a total of 5 steps, and of those 5 steps, 3 must be to the right (R), while 2 must be up (U). So that the problem is to figuring out how to arrange 3 R's and 2 U's in a sequence.

If we think about it, this is the same as figuring out how many ways we can choose 3 positions for the R's out of 5 total positions (the remaining positions will automatically be U's). This is a classic combination problem from discrete mathematics. We are choosing 3 steps out of 5 to be R's, and the formula for combinations is −

$$\mathrm{\binom{n}{k} \:=\: \frac{n!}{k!(n\:-\:k)!}}$$

In this case, we are choosing 3 Rs out of 5 steps, so −

$$\mathrm{\binom{5}{3} \:=\: \frac{5!}{3!(5\:-\:3)!} \:=\: \frac{5 \:\times\: 4 \:\times\: 3!}{3!2!} \:=\: \frac{5 \:\times \:4}{2!} \:=\: 10}$$

So, there are 10 possible lattice paths from (0, 0) to (3, 2).

Breaking It Down Further

Sometimes, it helps to break the problem into smaller segments. Consider if we are solving more complex grids or larger numbers. For example, imagine we are moving from (0, 0) to (3, 2) and we are curious about how many paths pass through a specific point along the way. Let us say the point is (2, 1).

To count the paths from (0, 0) to (3, 2) that pass through (2, 1), we can break the problem into two parts −

First, count how many paths go from (0, 0) to (2, 1). This is a 2-right and 1-up problem, which means there are −

$$\mathrm{\binom{3}{2} \:=\: \frac{3!}{2!(3\:-\:2)!} \:=\: \frac{3 \:\times\: 2}{2!} \:=\: 3}$$

2. Next, count how many paths go from (2, 1) to (3, 2). This is a 1-right and 1-up problem, which means theres only −

$$\mathrm{\binom{3}{2} \:=\: 2}$$

To get the total number of paths passing through (2, 1), we just multiply these two results −

$$\mathrm{3 \:\times\: 2 \:=\: 6 \text{ paths}}$$

By breaking it into two smaller steps, we have counted how many lattice paths go through a specific point.

Another View: Lattice Paths and Bit Strings

With lattice paths we can do some other interesting tasks as well. Counting lattice paths is actually very similar to another problem in discrete math: counting bit strings. The bit string is a sequence of 0s and 1s, just like a lattice path is a sequence of R’s and U’s.

Let us look back at our lattice path problem from (0, 0) to (3, 2). We needed to take exactly three R’s and two U’s, and we could arrange them in any order. Now, imagine replacing every R with a 1 and every U with a 0. So, we are not counting lattice paths anymore, we are counting bit strings of length 5, with exactly 3 ones and 2 zeroes. The number of bit strings like this is the same as the number of lattice paths, which we already know is 10.

This analogy between lattice paths and bit strings. This shows up often in discrete math, and it is a nice trick for solving problems in both areas.

Lattice Paths in Other Situations

We have seen how to count paths on a simple grid, but what we can do if the grid it not so simple. What if there are obstacles in the way, or the grid is a strange shape? The basic counting principles we can still apply. But the problem becomes a bit trickier.

Let us consider we are moving on a grid where some points are blocked off. Maybe we cannot step on certain squares, or maybe we can only move in specific directions. In these cases, we might need to break the problem into even smaller parts, just like we did when counting paths through (2, 1).

Sometimes, problems like these require even more advanced techniques, like dynamic programming or generating functions, to get the solution for the number of valid paths. But the core idea of counting problems will be the same. No matter how many ways we can arrange a sequence of steps. The results remains the same.

Conclusion

In this chapter, we explained the concept of lattice paths and how they work. We started with what lattice paths are and how they represent the shortest path between two points on a grid.

We then understood how to count the number of lattice paths between two points, first by using simple examples and then by breaking down the problem into smaller steps. Finally, we covered how lattice paths are closely related to bit strings.