ListConvolve returns only one value

Question

Generating my first function

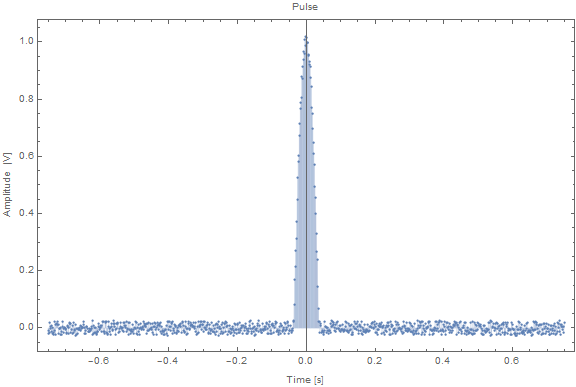
num = 1000; Amp = 0.05; time = 1.5; width = 0.1; T = 1.5; (*declaration of continous function*) With[{w = width, T = time}, pulse[x_] := Cos[2*Pi*x/(w*T)]*(UnitStep[x + w*T/4] - UnitStep[x - w*T/4])] (*funciton sampling*) funX = Table[i, {i, -T/2, T/2, T/(num - 1)}]; fun1 = pulse /@ funX + Amp*RandomReal[{-0.5, 0.5}, num]; ListPlot[Transpose[{funX, fun1}], PlotRange -> All, Filling -> Axis, Frame -> True, FrameLabel -> {"Time [s]", "Amplitude [V]", "Pulse"}, PlotLegends -> {"Pulse"}, ImageSize -> Large] 

and the second one

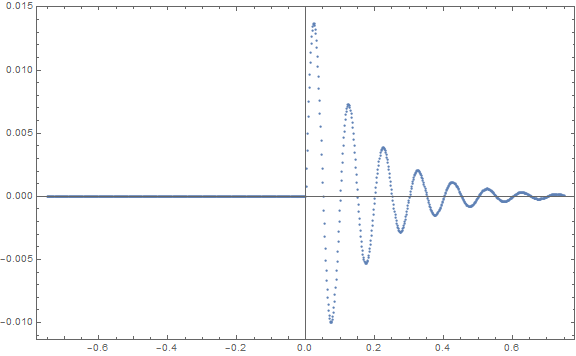
With[{\[Delta] = 0.1}, ImpulseResponse[t_] := (1/(2.0*Pi*10.0*Sqrt[1 - \[Delta]*\[Delta]]))* Exp[-\[Delta]*2.0*Pi*10.0*t]* Sin[2.0*Pi*10.0*Sqrt[1 - \[Delta]*\[Delta]]*t]*HeavisideTheta[t]] funTF = ImpulseResponse /@ funX; ListPlot[Transpose[{funX, funTF}], Frame -> True, PlotRange -> All, ImageSize -> Large] 

Now the plan was to follow this discussion using

 konv = ListConvolve[Transpose[{funX, funTF}], Transpose[{funX, fun1}]] (*{{0.152085}}*) 

but for some reason this doesn't work. The ListConvolve[] only returns one value instead of list. Any ideas why?

Answer 1

You need to tell ListConvolve how to handle "end conditions". Since your sequences are about the same length, everything is an end condition. Hence:

ListPlot[ListConvolve[funTF, funX, {1, -1}]] 

will give the circular convolution of the sequences funX and funTF. There are several other choices for the pair of numbers (like {1,-1}) or you can directly specify the desired length of the output. You can read more about these optional arguments in the Details section of the help file.

From your comment, I guess you are expecting linear (rather than circular) convolution. You can do this by zeropadding. For example:

zeropad = Flatten[{ConstantArray[0, Length[funTF]], funX, ConstantArray[0, Length[funTF]]}]; ListPlot[ListConvolve[funTF, zeropad, {1, -1}], PlotRange -> All]