Magic Square with Five Methods (Python)

Question

Problem

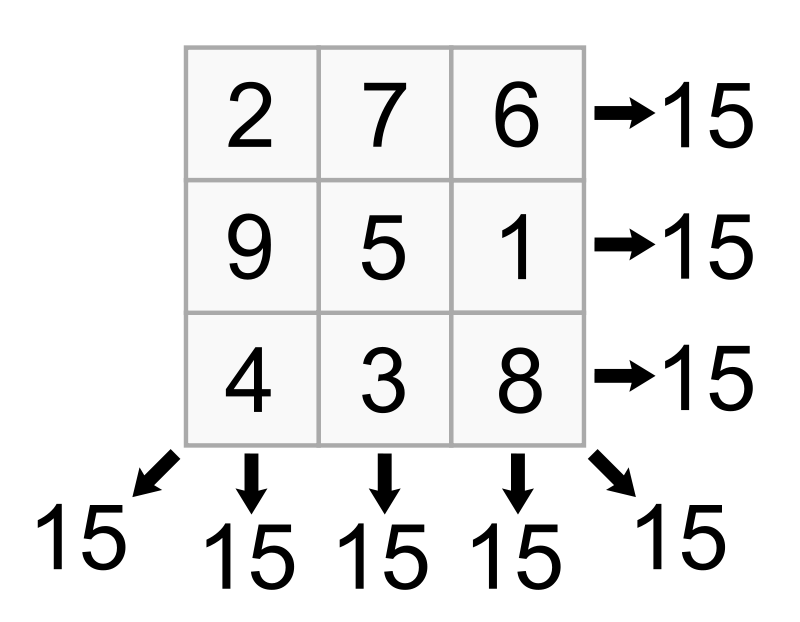
Write a program to return a boolean if an input grid is magic square.

---

A magic square of order \$N\$ is an arrangement of \$N^2\$ distinct integers in a square such that the \$N\$ numbers in all rows and columns and both diagonals sum to the same constant, known as magic sum or magic constant, \$magic\_sum\$. A magic square contains the integers from \$1\$ to \$N^2\$.

The magic sum of a normal magic square depends only on one variable, \$N\$:

\$magic\_sum = \dfrac{N(N^2+1)}{2}\$

Code

We've solved "if a grid is magic square" problem with five methods, which I've just slightly modified those and included timeit benchmarking. If you would like to review the code, or add other methods or anything else or provide any change/improvement recommendations please do so, and I'd really appreciate that.

import numpy as np from typing import List, Iterable, Callable from functools import partial Grid = List[List[int]] # Might as well create an alias for this def has_correct_dimensions(grid: Grid) -> bool: """Returns whether or not the grid is a non-jagged square.""" return all(len(row) == len(grid) for row in grid) def is_normal_square(grid: Grid) -> bool: """Returns whether or not the function contains unique numbers from 1 to n**2.""" max_n = len(grid[0]) ** 2 # Does the set of numbers in the flattened grid contain the same numbers as a range set from 1 to n**2? return set(e for row in grid for e in row) == set(range(1, max_n + 1)) def check_each(iterable: Iterable[Iterable[int]], magic_sum: int) -> bool: """Returns whether or not every sub-iterable collection sums to the magic sum""" return all(sum(elem) == magic_sum for elem in iterable) def diagonal_of(grid: Grid, y_indexer: Callable[[int], int]) -> Iterable[int]: """Generates a line of elements from the grid. y = y_indexer(x).""" return (grid[y_indexer(x)][x] for x in range(len(grid))) def magic_constant(grid: Grid) -> int: """Returns the magic sum integer value""" return len(grid) * (len(grid) ** 2 + 1) / 2 def is_magic_square_multifunctions(grid: Grid) -> bool: """Returns whether or not the supplied grid is a proper normal magic square.""" magic_sum = magic_constant(grid) check = partial(check_each, magic_sum=magic_sum) return is_normal_square(grid) and \ has_correct_dimensions(grid) and \ check(grid) and \ check(zip(*grid)) and \ check([diagonal_of(grid, lambda x: x), diagonal_of(grid, lambda x: len(grid) - x - 1)]) def is_magic_square_linguini(grid: Grid) -> bool: length = len(grid) if length == 0: return False magic_sum = magic_constant(grid) sum_three, sum_four = int(), int() for index_row in range(length): sum_one, sum_two = int(), int() unique_elements = dict() for index_col in range(length): if grid[index_row][index_col] in unique_elements: return False unique_elements[grid[index_row][index_col]] = True sum_one += grid[index_row][index_col] sum_two += grid[index_col][index_row] if index_row == index_col: sum_three += grid[index_col][index_row] if (index_row + index_col) == length - 1: sum_four += grid[index_row][index_col] if sum_one != magic_sum or sum_two != magic_sum: return False if sum_three != magic_sum or sum_four != magic_sum: return False return True def is_magic_square_vermicelli(grid: List[List[int]]) -> bool: """Returns a boolean if an input grid is magic square""" grid_length = len(grid) magic_sum = magic_constant(grid) diag_positive, diag_negative = [], [] diag_count_positive, diag_count_negative = 0, grid_length - 1 col_grid = np.zeros(shape=(grid_length, grid_length)) unique_elements = set() for index_row, lists in enumerate(grid): diag_negative.append(lists[diag_count_negative]) diag_count_negative -= 1 if len(grid[index_row]) != grid_length: return False if sum(lists) != magic_sum: return False for index_col in range(grid_length): unique_elements.add(lists[index_col]) col_grid[index_col][index_row] = lists[index_col] if index_col == grid_length and index_row == grid_length - 1 and len(unique_elements) != grid_length ** 2 - 1: return False if index_row == grid_length - 1: sum_col, temp_col = sum(col_grid), np.array( [magic_sum] * grid_length) if str(temp_col) != str(sum_col): return False if diag_count_positive == index_row: diag_positive.append(lists[index_row]) diag_count_positive += 1 if diag_count_positive == grid_length and sum(diag_positive) != magic_sum: return False if index_row == grid_length - 1 and sum(diag_negative) != magic_sum: return False return True def is_magic_square_single_method(grid: List[List[int]]) -> bool: """Returns a boolean if an input grid is magic square""" grid_length = len(grid) grid_area = grid_length ** 2 magic_sum = magic_constant(grid) # check the length of all rows if any(len(row) != grid_length for row in grid): return False # check it has all the numbers in sequence if set(x for row in grid for x in row) != set(range(1, grid_area + 1)): return False # check all the rows add up to the magic_number if any(sum(row) != magic_sum for row in grid): return False # check all the columns add up to the magic_number if any(sum(row[col] for row in grid) != magic_sum for col in range(grid_length)): return False # check each diagonal adds up to the magic_number if (sum(grid[i][i] for i in range(grid_length)) != magic_sum or sum(grid[i][grid_length - i - 1] for i in range(grid_length)) != magic_sum): return False return True def is_magic_square_numpy(grid: List[List[int]]) -> bool: """Returns a boolean if an input grid is magic square""" grid_length = len(grid) magic_sum = magic_constant(grid) # check the length of all rows if any(len(row) != grid_length for row in grid): return False npgrid = np.array(grid) # check it has all ints from 1 to grid_length**2 (inclusive) if len(np.setdiff1d(npgrid, np.arange(1, grid_length ** 2 + 1))): return False # check all the rows add up to the magic_number if any(np.not_equal(npgrid.sum(axis=0), magic_sum)): return False # check all the columns add up to the magic_number if any(np.not_equal(npgrid.sum(axis=1), magic_sum)): return False # check both diagonals add up to the magic_number if (npgrid.diagonal().sum() != magic_sum or np.fliplr(npgrid).diagonal().sum() != magic_sum): return False return True if __name__ == '__main__': # ---------------------------- TEST --------------------------- import timeit import cProfile DIVIDER_DASH_LINE = '-' * 50 GREEN_APPLE = '\U0001F34F' RED_APPLE = '\U0001F34E' magic_squares = ( [[4, 3, 8], [9, 5, 1], [2, 7, 6]], [[8, 1, 6], [3, 5, 7], [4, 9, 2]], [[1, 14, 4, 15], [8, 11, 5, 10], [13, 2, 16, 3], [12, 7, 9, 6]], [[9, 3, 22, 16, 15], [2, 21, 20, 14, 8], [25, 19, 13, 7, 1], [18, 12, 6, 5, 24], [11, 10, 4, 23, 17]], [[16, 14, 7, 30, 23], [24, 17, 10, 8, 31], [32, 25, 18, 11, 4], [5, 28, 26, 19, 12], [13, 6, 29, 22, 20]], [[1, 35, 4, 33, 32, 6], [25, 11, 9, 28, 8, 30], [24, 14, 18, 16, 17, 22], [13, 23, 19, 21, 20, 15], [12, 26, 27, 10, 29, 7], [36, 2, 34, 3, 5, 31]], [[35, 26, 17, 1, 62, 53, 44], [46, 37, 21, 12, 3, 64, 55], [57, 41, 32, 23, 14, 5, 66], [61, 52, 43, 34, 25, 16, 7], [2, 63, 54, 45, 36, 27, 11], [13, 4, 65, 56, 47, 31, 22], [24, 15, 6, 67, 51, 42, 33]], [[60, 53, 44, 37, 4, 13, 20, 29], [3, 14, 19, 30, 59, 54, 43, 38], [58, 55, 42, 39, 2, 15, 18, 31], [1, 16, 17, 32, 57, 56, 41, 40], [61, 52, 45, 36, 5, 12, 21, 28], [6, 11, 22, 27, 62, 51, 46, 35], [63, 50, 47, 34, 7, 10, 23, 26], [8, 9, 24, 25, 64, 49, 48, 33]], [[22, 47, 16, 41, 10, 35, 4], [5, 23, 48, 17, 42, 11, 29], [30, 6, 24, 49, 18, 36, 12], [13, 31, 7, 25, 43, 19, 37], [38, 14, 32, 1, 26, 44, 20], [21, 39, 8, 33, 2, 27, 45], [46, 15, 40, 9, 34, 3, 28]], [[8, 58, 59, 5, 4, 62, 63, 1], [49, 15, 14, 52, 53, 11, 10, 56], [41, 23, 22, 44, 45, 19, 18, 48], [32, 34, 35, 29, 28, 38, 39, 25], [40, 26, 27, 37, 36, 30, 31, 33], [17, 47, 46, 20, 21, 43, 42, 24], [9, 55, 54, 12, 13, 51, 50, 16], [64, 2, 3, 61, 60, 6, 7, 57]], [[37, 78, 29, 70, 21, 62, 13, 54, 5], [6, 38, 79, 30, 71, 22, 63, 14, 46], [47, 7, 39, 80, 31, 72, 23, 55, 15], [16, 48, 8, 40, 81, 32, 64, 24, 56], [57, 17, 49, 9, 41, 73, 33, 65, 25], [26, 58, 18, 50, 1, 42, 74, 34, 66], [67, 27, 59, 10, 51, 2, 43, 75, 35], [36, 68, 19, 60, 11, 52, 3, 44, 76], [77, 28, 69, 20, 61, 12, 53, 4, 45]], ) test_methods = ( ("Multifunctions", is_magic_square_multifunctions), ("Linguine", is_magic_square_linguini), ("Vermicelli", is_magic_square_vermicelli), ("Single Method", is_magic_square_single_method), ("Numpy", is_magic_square_numpy), ) # --------------------------------- PROFILING AND BANCHMARK SETTINGS -------------------------------------- NUMBER_OF_RUNS = 64 CPROFILING_ON = False BENCHMARK_ON = True for description, method in test_methods: print((GREEN_APPLE + RED_APPLE) * 5) for magic_square in magic_squares: if CPROFILING_ON is True: print(f'{description} cProfiling: ', cProfile.run("method(magic_square)")) if BENCHMARK_ON is True: print(f'{description} Benchmark: ', timeit.Timer( f'for i in range({NUMBER_OF_RUNS}): {method(magic_square)}', 'gc.enable()').timeit()) if method(magic_square) is True: print(f'{GREEN_APPLE} {description}: "{magic_square}" is a magic square.') else: print(f'{RED_APPLE} {description}: "{magic_square}" is not a magic square.') 

Test

These variables can be assigned differently for testing:

NUMBER_OF_RUNS = 64 CPROFILING_ON = False BENCHMARK_ON = True 

A Sample Output

🍏🍎🍏🍎🍏🍎🍏🍎🍏🍎 Multifunctions Benchmark: 5.588784874 🍏 Multifunctions: "[[4, 3, 8], [9, 5, 1], [2, 7, 6]]" is a magic square. Multifunctions Benchmark: 5.549960512000001 🍏 Multifunctions: "[[8, 1, 6], [3, 5, 7], [4, 9, 2]]" is a magic square. Multifunctions Benchmark: 5.783070463 🍏 Multifunctions: "[[1, 14, 4, 15], [8, 11, 5, 10], [13, 2, 16, 3], [12, 7, 9, 6]]" is a magic square. Multifunctions Benchmark: 6.041834480999999 🍏 Multifunctions: "[[9, 3, 22, 16, 15], [2, 21, 20, 14, 8], [25, 19, 13, 7, 1], [18, 12, 6, 5, 24], [11, 10, 4, 23, 17]]" is a magic square. Multifunctions Benchmark: 6.304372493999999 🍎 Multifunctions: "[[16, 14, 7, 30, 23], [24, 17, 10, 8, 31], [32, 25, 18, 11, 4], [5, 28, 26, 19, 12], [13, 6, 29, 22, 20]]" is not a magic square. Multifunctions Benchmark: 6.737646978000001 🍏 Multifunctions: "[[1, 35, 4, 33, 32, 6], [25, 11, 9, 28, 8, 30], [24, 14, 18, 16, 17, 22], [13, 23, 19, 21, 20, 15], [12, 26, 27, 10, 29, 7], [36, 2, 34, 3, 5, 31]]" is a magic square. Multifunctions Benchmark: 6.330970278999999 🍎 Multifunctions: "[[35, 26, 17, 1, 62, 53, 44], [46, 37, 21, 12, 3, 64, 55], [57, 41, 32, 23, 14, 5, 66], [61, 52, 43, 34, 25, 16, 7], [2, 63, 54, 45, 36, 27, 11], [13, 4, 65, 56, 47, 31, 22], [24, 15, 6, 67, 51, 42, 33]]" is not a magic square. Multifunctions Benchmark: 6.320764873000002 🍏 Multifunctions: "[[60, 53, 44, 37, 4, 13, 20, 29], [3, 14, 19, 30, 59, 54, 43, 38], [58, 55, 42, 39, 2, 15, 18, 31], [1, 16, 17, 32, 57, 56, 41, 40], [61, 52, 45, 36, 5, 12, 21, 28], [6, 11, 22, 27, 62, 51, 46, 35], [63, 50, 47, 34, 7, 10, 23, 26], [8, 9, 24, 25, 64, 49, 48, 33]]" is a magic square. Multifunctions Benchmark: 6.070653400000005 🍏 Multifunctions: "[[22, 47, 16, 41, 10, 35, 4], [5, 23, 48, 17, 42, 11, 29], [30, 6, 24, 49, 18, 36, 12], [13, 31, 7, 25, 43, 19, 37], [38, 14, 32, 1, 26, 44, 20], [21, 39, 8, 33, 2, 27, 45], [46, 15, 40, 9, 34, 3, 28]]" is a magic square. Multifunctions Benchmark: 5.944438742000003 🍏 Multifunctions: "[[8, 58, 59, 5, 4, 62, 63, 1], [49, 15, 14, 52, 53, 11, 10, 56], [41, 23, 22, 44, 45, 19, 18, 48], [32, 34, 35, 29, 28, 38, 39, 25], [40, 26, 27, 37, 36, 30, 31, 33], [17, 47, 46, 20, 21, 43, 42, 24], [9, 55, 54, 12, 13, 51, 50, 16], [64, 2, 3, 61, 60, 6, 7, 57]]" is a magic square. Multifunctions Benchmark: 5.747417926999994 🍏 Multifunctions: "[[37, 78, 29, 70, 21, 62, 13, 54, 5], [6, 38, 79, 30, 71, 22, 63, 14, 46], [47, 7, 39, 80, 31, 72, 23, 55, 15], [16, 48, 8, 40, 81, 32, 64, 24, 56], [57, 17, 49, 9, 41, 73, 33, 65, 25], [26, 58, 18, 50, 1, 42, 74, 34, 66], [67, 27, 59, 10, 51, 2, 43, 75, 35], [36, 68, 19, 60, 11, 52, 3, 44, 76], [77, 28, 69, 20, 61, 12, 53, 4, 45]]" is a magic square. 🍏🍎🍏🍎🍏🍎🍏🍎🍏🍎 Linguine Benchmark: 5.696244382999993 🍏 Linguine: "[[4, 3, 8], [9, 5, 1], [2, 7, 6]]" is a magic square. Linguine Benchmark: 5.674139272000005 🍏 Linguine: "[[8, 1, 6], [3, 5, 7], [4, 9, 2]]" is a magic square. Linguine Benchmark: 5.92109452599999 🍏 Linguine: "[[1, 14, 4, 15], [8, 11, 5, 10], [13, 2, 16, 3], [12, 7, 9, 6]]" is a magic square. Linguine Benchmark: 5.958363641999995 🍏 Linguine: "[[9, 3, 22, 16, 15], [2, 21, 20, 14, 8], [25, 19, 13, 7, 1], [18, 12, 6, 5, 24], [11, 10, 4, 23, 17]]" is a magic square. Linguine Benchmark: 5.686515516 🍎 Linguine: "[[16, 14, 7, 30, 23], [24, 17, 10, 8, 31], [32, 25, 18, 11, 4], [5, 28, 26, 19, 12], [13, 6, 29, 22, 20]]" is not a magic square. Linguine Benchmark: 5.728992446999996 🍏 Linguine: "[[1, 35, 4, 33, 32, 6], [25, 11, 9, 28, 8, 30], [24, 14, 18, 16, 17, 22], [13, 23, 19, 21, 20, 15], [12, 26, 27, 10, 29, 7], [36, 2, 34, 3, 5, 31]]" is a magic square. Linguine Benchmark: 5.650582772000007 🍎 Linguine: "[[35, 26, 17, 1, 62, 53, 44], [46, 37, 21, 12, 3, 64, 55], [57, 41, 32, 23, 14, 5, 66], [61, 52, 43, 34, 25, 16, 7], [2, 63, 54, 45, 36, 27, 11], [13, 4, 65, 56, 47, 31, 22], [24, 15, 6, 67, 51, 42, 33]]" is not a magic square. Linguine Benchmark: 5.616721932000004 🍏 Linguine: "[[60, 53, 44, 37, 4, 13, 20, 29], [3, 14, 19, 30, 59, 54, 43, 38], [58, 55, 42, 39, 2, 15, 18, 31], [1, 16, 17, 32, 57, 56, 41, 40], [61, 52, 45, 36, 5, 12, 21, 28], [6, 11, 22, 27, 62, 51, 46, 35], [63, 50, 47, 34, 7, 10, 23, 26], [8, 9, 24, 25, 64, 49, 48, 33]]" is a magic square. Linguine Benchmark: 5.492888303000001 🍏 Linguine: "[[22, 47, 16, 41, 10, 35, 4], [5, 23, 48, 17, 42, 11, 29], [30, 6, 24, 49, 18, 36, 12], [13, 31, 7, 25, 43, 19, 37], [38, 14, 32, 1, 26, 44, 20], [21, 39, 8, 33, 2, 27, 45], [46, 15, 40, 9, 34, 3, 28]]" is a magic square. Linguine Benchmark: 5.574545161999993 🍏 Linguine: "[[8, 58, 59, 5, 4, 62, 63, 1], [49, 15, 14, 52, 53, 11, 10, 56], [41, 23, 22, 44, 45, 19, 18, 48], [32, 34, 35, 29, 28, 38, 39, 25], [40, 26, 27, 37, 36, 30, 31, 33], [17, 47, 46, 20, 21, 43, 42, 24], [9, 55, 54, 12, 13, 51, 50, 16], [64, 2, 3, 61, 60, 6, 7, 57]]" is a magic square. Linguine Benchmark: 5.479747597999989 🍏 Linguine: "[[37, 78, 29, 70, 21, 62, 13, 54, 5], [6, 38, 79, 30, 71, 22, 63, 14, 46], [47, 7, 39, 80, 31, 72, 23, 55, 15], [16, 48, 8, 40, 81, 32, 64, 24, 56], [57, 17, 49, 9, 41, 73, 33, 65, 25], [26, 58, 18, 50, 1, 42, 74, 34, 66], [67, 27, 59, 10, 51, 2, 43, 75, 35], [36, 68, 19, 60, 11, 52, 3, 44, 76], [77, 28, 69, 20, 61, 12, 53, 4, 45]]" is a magic square. 🍏🍎🍏🍎🍏🍎🍏🍎🍏🍎 Vermicelli Benchmark: 5.610320167999987 🍏 Vermicelli: "[[4, 3, 8], [9, 5, 1], [2, 7, 6]]" is a magic square. Vermicelli Benchmark: 5.473386472000016 🍏 Vermicelli: "[[8, 1, 6], [3, 5, 7], [4, 9, 2]]" is a magic square. Vermicelli Benchmark: 5.50186076 🍏 Vermicelli: "[[1, 14, 4, 15], [8, 11, 5, 10], [13, 2, 16, 3], [12, 7, 9, 6]]" is a magic square. Vermicelli Benchmark: 5.465219862999987 🍏 Vermicelli: "[[9, 3, 22, 16, 15], [2, 21, 20, 14, 8], [25, 19, 13, 7, 1], [18, 12, 6, 5, 24], [11, 10, 4, 23, 17]]" is a magic square. Vermicelli Benchmark: 5.538681058999998 🍎 Vermicelli: "[[16, 14, 7, 30, 23], [24, 17, 10, 8, 31], [32, 25, 18, 11, 4], [5, 28, 26, 19, 12], [13, 6, 29, 22, 20]]" is not a magic square. Vermicelli Benchmark: 5.466972800000008 🍏 Vermicelli: "[[1, 35, 4, 33, 32, 6], [25, 11, 9, 28, 8, 30], [24, 14, 18, 16, 17, 22], [13, 23, 19, 21, 20, 15], [12, 26, 27, 10, 29, 7], [36, 2, 34, 3, 5, 31]]" is a magic square. Vermicelli Benchmark: 5.542082810000011 🍎 Vermicelli: "[[35, 26, 17, 1, 62, 53, 44], [46, 37, 21, 12, 3, 64, 55], [57, 41, 32, 23, 14, 5, 66], [61, 52, 43, 34, 25, 16, 7], [2, 63, 54, 45, 36, 27, 11], [13, 4, 65, 56, 47, 31, 22], [24, 15, 6, 67, 51, 42, 33]]" is not a magic square. Vermicelli Benchmark: 5.477112298999998 🍏 Vermicelli: "[[60, 53, 44, 37, 4, 13, 20, 29], [3, 14, 19, 30, 59, 54, 43, 38], [58, 55, 42, 39, 2, 15, 18, 31], [1, 16, 17, 32, 57, 56, 41, 40], [61, 52, 45, 36, 5, 12, 21, 28], [6, 11, 22, 27, 62, 51, 46, 35], [63, 50, 47, 34, 7, 10, 23, 26], [8, 9, 24, 25, 64, 49, 48, 33]]" is a magic square. Vermicelli Benchmark: 5.534445683000001 🍏 Vermicelli: "[[22, 47, 16, 41, 10, 35, 4], [5, 23, 48, 17, 42, 11, 29], [30, 6, 24, 49, 18, 36, 12], [13, 31, 7, 25, 43, 19, 37], [38, 14, 32, 1, 26, 44, 20], [21, 39, 8, 33, 2, 27, 45], [46, 15, 40, 9, 34, 3, 28]]" is a magic square. Vermicelli Benchmark: 5.473650165999999 🍏 Vermicelli: "[[8, 58, 59, 5, 4, 62, 63, 1], [49, 15, 14, 52, 53, 11, 10, 56], [41, 23, 22, 44, 45, 19, 18, 48], [32, 34, 35, 29, 28, 38, 39, 25], [40, 26, 27, 37, 36, 30, 31, 33], [17, 47, 46, 20, 21, 43, 42, 24], [9, 55, 54, 12, 13, 51, 50, 16], [64, 2, 3, 61, 60, 6, 7, 57]]" is a magic square. Vermicelli Benchmark: 5.516359977000008 🍏 Vermicelli: "[[37, 78, 29, 70, 21, 62, 13, 54, 5], [6, 38, 79, 30, 71, 22, 63, 14, 46], [47, 7, 39, 80, 31, 72, 23, 55, 15], [16, 48, 8, 40, 81, 32, 64, 24, 56], [57, 17, 49, 9, 41, 73, 33, 65, 25], [26, 58, 18, 50, 1, 42, 74, 34, 66], [67, 27, 59, 10, 51, 2, 43, 75, 35], [36, 68, 19, 60, 11, 52, 3, 44, 76], [77, 28, 69, 20, 61, 12, 53, 4, 45]]" is a magic square. 🍏🍎🍏🍎🍏🍎🍏🍎🍏🍎 Single Method Benchmark: 5.792159653999988 🍏 Single Method: "[[4, 3, 8], [9, 5, 1], [2, 7, 6]]" is a magic square. Single Method Benchmark: 5.452938262999993 🍏 Single Method: "[[8, 1, 6], [3, 5, 7], [4, 9, 2]]" is a magic square. Single Method Benchmark: 5.8117709149999826 🍏 Single Method: "[[1, 14, 4, 15], [8, 11, 5, 10], [13, 2, 16, 3], [12, 7, 9, 6]]" is a magic square. Single Method Benchmark: 5.46323830099999 🍏 Single Method: "[[9, 3, 22, 16, 15], [2, 21, 20, 14, 8], [25, 19, 13, 7, 1], [18, 12, 6, 5, 24], [11, 10, 4, 23, 17]]" is a magic square. Single Method Benchmark: 5.8472462789999895 🍎 Single Method: "[[16, 14, 7, 30, 23], [24, 17, 10, 8, 31], [32, 25, 18, 11, 4], [5, 28, 26, 19, 12], [13, 6, 29, 22, 20]]" is not a magic square. Single Method Benchmark: 5.433652160999998 🍏 Single Method: "[[1, 35, 4, 33, 32, 6], [25, 11, 9, 28, 8, 30], [24, 14, 18, 16, 17, 22], [13, 23, 19, 21, 20, 15], [12, 26, 27, 10, 29, 7], [36, 2, 34, 3, 5, 31]]" is a magic square. Single Method Benchmark: 5.805129637999983 🍎 Single Method: "[[35, 26, 17, 1, 62, 53, 44], [46, 37, 21, 12, 3, 64, 55], [57, 41, 32, 23, 14, 5, 66], [61, 52, 43, 34, 25, 16, 7], [2, 63, 54, 45, 36, 27, 11], [13, 4, 65, 56, 47, 31, 22], [24, 15, 6, 67, 51, 42, 33]]" is not a magic square. Single Method Benchmark: 5.48093770700001 🍏 Single Method: "[[60, 53, 44, 37, 4, 13, 20, 29], [3, 14, 19, 30, 59, 54, 43, 38], [58, 55, 42, 39, 2, 15, 18, 31], [1, 16, 17, 32, 57, 56, 41, 40], [61, 52, 45, 36, 5, 12, 21, 28], [6, 11, 22, 27, 62, 51, 46, 35], [63, 50, 47, 34, 7, 10, 23, 26], [8, 9, 24, 25, 64, 49, 48, 33]]" is a magic square. Single Method Benchmark: 5.818483440999984 🍏 Single Method: "[[22, 47, 16, 41, 10, 35, 4], [5, 23, 48, 17, 42, 11, 29], [30, 6, 24, 49, 18, 36, 12], [13, 31, 7, 25, 43, 19, 37], [38, 14, 32, 1, 26, 44, 20], [21, 39, 8, 33, 2, 27, 45], [46, 15, 40, 9, 34, 3, 28]]" is a magic square. Single Method Benchmark: 5.494786433999991 🍏 Single Method: "[[8, 58, 59, 5, 4, 62, 63, 1], [49, 15, 14, 52, 53, 11, 10, 56], [41, 23, 22, 44, 45, 19, 18, 48], [32, 34, 35, 29, 28, 38, 39, 25], [40, 26, 27, 37, 36, 30, 31, 33], [17, 47, 46, 20, 21, 43, 42, 24], [9, 55, 54, 12, 13, 51, 50, 16], [64, 2, 3, 61, 60, 6, 7, 57]]" is a magic square. Single Method Benchmark: 5.769875240999994 🍏 Single Method: "[[37, 78, 29, 70, 21, 62, 13, 54, 5], [6, 38, 79, 30, 71, 22, 63, 14, 46], [47, 7, 39, 80, 31, 72, 23, 55, 15], [16, 48, 8, 40, 81, 32, 64, 24, 56], [57, 17, 49, 9, 41, 73, 33, 65, 25], [26, 58, 18, 50, 1, 42, 74, 34, 66], [67, 27, 59, 10, 51, 2, 43, 75, 35], [36, 68, 19, 60, 11, 52, 3, 44, 76], [77, 28, 69, 20, 61, 12, 53, 4, 45]]" is a magic square. 🍏🍎🍏🍎🍏🍎🍏🍎🍏🍎 Numpy Benchmark: 5.541609400999988 🍏 Numpy: "[[4, 3, 8], [9, 5, 1], [2, 7, 6]]" is a magic square. Numpy Benchmark: 5.829946971000027 🍏 Numpy: "[[8, 1, 6], [3, 5, 7], [4, 9, 2]]" is a magic square. Numpy Benchmark: 5.444178211999997 🍏 Numpy: "[[1, 14, 4, 15], [8, 11, 5, 10], [13, 2, 16, 3], [12, 7, 9, 6]]" is a magic square. Numpy Benchmark: 5.820747697000002 🍏 Numpy: "[[9, 3, 22, 16, 15], [2, 21, 20, 14, 8], [25, 19, 13, 7, 1], [18, 12, 6, 5, 24], [11, 10, 4, 23, 17]]" is a magic square. Numpy Benchmark: 5.5407621650000465 🍎 Numpy: "[[16, 14, 7, 30, 23], [24, 17, 10, 8, 31], [32, 25, 18, 11, 4], [5, 28, 26, 19, 12], [13, 6, 29, 22, 20]]" is not a magic square. Numpy Benchmark: 5.764756991000013 🍏 Numpy: "[[1, 35, 4, 33, 32, 6], [25, 11, 9, 28, 8, 30], [24, 14, 18, 16, 17, 22], [13, 23, 19, 21, 20, 15], [12, 26, 27, 10, 29, 7], [36, 2, 34, 3, 5, 31]]" is a magic square. Numpy Benchmark: 5.588026968999998 🍎 Numpy: "[[35, 26, 17, 1, 62, 53, 44], [46, 37, 21, 12, 3, 64, 55], [57, 41, 32, 23, 14, 5, 66], [61, 52, 43, 34, 25, 16, 7], [2, 63, 54, 45, 36, 27, 11], [13, 4, 65, 56, 47, 31, 22], [24, 15, 6, 67, 51, 42, 33]]" is not a magic square. Numpy Benchmark: 5.712816462999967 🍏 Numpy: "[[60, 53, 44, 37, 4, 13, 20, 29], [3, 14, 19, 30, 59, 54, 43, 38], [58, 55, 42, 39, 2, 15, 18, 31], [1, 16, 17, 32, 57, 56, 41, 40], [61, 52, 45, 36, 5, 12, 21, 28], [6, 11, 22, 27, 62, 51, 46, 35], [63, 50, 47, 34, 7, 10, 23, 26], [8, 9, 24, 25, 64, 49, 48, 33]]" is a magic square. Numpy Benchmark: 5.540658426999983 🍏 Numpy: "[[22, 47, 16, 41, 10, 35, 4], [5, 23, 48, 17, 42, 11, 29], [30, 6, 24, 49, 18, 36, 12], [13, 31, 7, 25, 43, 19, 37], [38, 14, 32, 1, 26, 44, 20], [21, 39, 8, 33, 2, 27, 45], [46, 15, 40, 9, 34, 3, 28]]" is a magic square. Numpy Benchmark: 5.761296496999989 🍏 Numpy: "[[8, 58, 59, 5, 4, 62, 63, 1], [49, 15, 14, 52, 53, 11, 10, 56], [41, 23, 22, 44, 45, 19, 18, 48], [32, 34, 35, 29, 28, 38, 39, 25], [40, 26, 27, 37, 36, 30, 31, 33], [17, 47, 46, 20, 21, 43, 42, 24], [9, 55, 54, 12, 13, 51, 50, 16], [64, 2, 3, 61, 60, 6, 7, 57]]" is a magic square. Numpy Benchmark: 5.583522877999997 🍏 Numpy: "[[37, 78, 29, 70, 21, 62, 13, 54, 5], [6, 38, 79, 30, 71, 22, 63, 14, 46], [47, 7, 39, 80, 31, 72, 23, 55, 15], [16, 48, 8, 40, 81, 32, 64, 24, 56], [57, 17, 49, 9, 41, 73, 33, 65, 25], [26, 58, 18, 50, 1, 42, 74, 34, 66], [67, 27, 59, 10, 51, 2, 43, 75, 35], [36, 68, 19, 60, 11, 52, 3, 44, 76], [77, 28, 69, 20, 61, 12, 53, 4, 45]]" is a magic square. 

Source

• Magic Square (Python)

• Magic Squares In Grid - LeetCode

• Magic Square - Geeks for Geeks

Answer 1

Overall this is quite reasonable. Good job!

Boolean conditions

No need to write

 if CPROFILING_ON is True: 

Just write

 if CPROFILING_ON: 

Int constructor

This:

 sum_one, sum_two = int(), int() 

is just a goofier way of writing

 sum_one, sum_two = 0, 0 

The latter is clearer.

Set instead of dict

unique_elements should be a set, not a dict. You never use the value, just the key.

Line continuations

return is_normal_square(grid) and \ has_correct_dimensions(grid) and \ check(grid) and \ check(zip(*grid)) and \ check([diagonal_of(grid, lambda x: x), diagonal_of(grid, lambda x: len(grid) - x - 1)]) 

has a lot of continuations; preferred is usually

return ( is_normal_square(grid) and has_correct_dimensions(grid) and check(grid) and check(zip(*grid)) and check([diagonal_of(grid, lambda x: x), diagonal_of(grid, lambda x: len(grid) - x - 1)]) ) 

Answer 2

Here's a solution with conditional returns. A benefit with this approach is that it saves time by not doing a full check as soon as a non-magic property is discovered. This function takes square as a list of lists (rows).

from typing import List def is_really_magic(square: List[List[int]]) -> bool: dim = len(square) magic_const = dim * (dim**2 +1) // 2 dia_sum = 0 dia_sum2 = 0 for y in range(dim): if sum(square[y]) != magic_const: return False col_sum = 0 for row in square: col_sum += row[y] if col_sum != magic_const: return False dia_sum += square[y][y] dia_sum2 += square[y][dim-1-y] if dia_sum != magic_const or dia_sum2 != magic_const: return False return True