Magic Square (Python)

Question

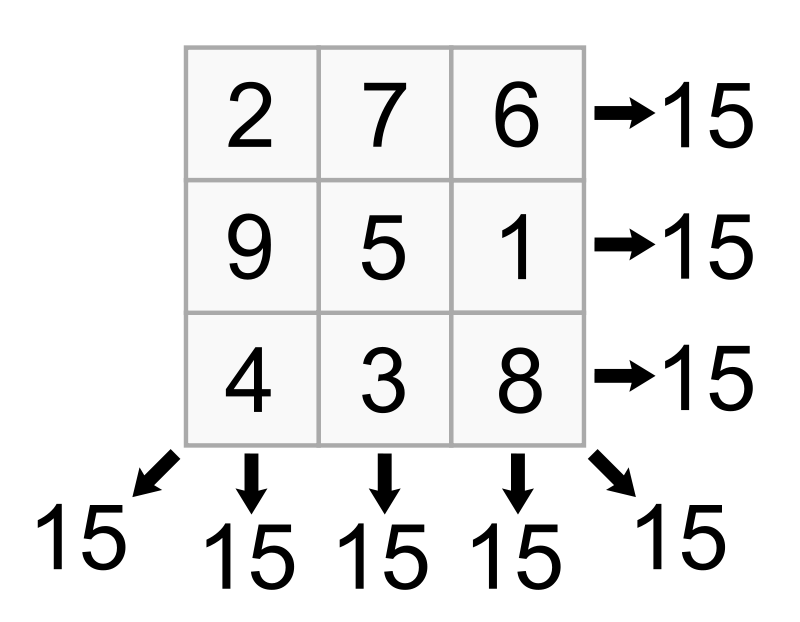
Problem

Write a method to return a boolean if an input grid is magic square.

---

A magic square is a \$NxN\$ square grid (where N is the number of cells on each side) filled with distinct positive integers in the range \${1,2,...,n^{2}}\$ such that each cell contains a different integer and the sum of the integers in each row, column and diagonal is equal. The sum is called the magic constant or magic sum of the magic square.

---

Code

I've tried to solve the above problem. If you'd like to review the code and provide any change/improvement recommendations please do so, and I'd really appreciate that.

from typing import List import numpy as np def is_magic_square(grid: List[List[int]]) -> bool: """Returns a boolean if an input grid is magic square""" try: grid_length = len(grid) magic_sum = float(grid_length * (grid_length ** 2 + 1) / 2) diag_positive, diag_negative = [], [] diag_count_positive = 0 diag_count_negative = grid_length - 1 col_grid = np.zeros(shape=(grid_length, grid_length)) unique_elements = set() for index_row, lists in enumerate(grid): diag_negative.append(lists[diag_count_negative]) diag_count_negative -= 1 if len(grid[index_row]) != grid_length: return False if sum(lists) != magic_sum: return False for index_col in range(grid_length): unique_elements.add(lists[index_col]) col_grid[index_col][index_row] = lists[index_col] if index_col == grid_length and index_row == grid_length - 1 and len(unique_elements) != grid_length ** 2 - 1: return False if index_row == grid_length - 1: sum_col = sum(col_grid) temp_col = np.array([magic_sum] * grid_length) if str(temp_col) != str(sum_col): return False if diag_count_positive == index_row: diag_positive.append(lists[index_row]) diag_count_positive += 1 if diag_count_positive == grid_length and sum(diag_positive) != magic_sum: return False if index_row == grid_length - 1 and sum(diag_negative) != magic_sum: return False except: return False return True if __name__ == '__main__': # ---------------------------- TEST --------------------------- DIVIDER_DASH_LINE = '-' * 50 GREEN_APPLE = '\U0001F34F' RED_APPLE = '\U0001F34E' magic_squares = [ [[4, 3, 8], [9, 5, 1], [2, 7, 6]], [[9, 3, 22, 16, 15], [2, 21, 20, 14, 8], [25, 19, 13, 7, 1], [18, 12, 6, 5, 24], [11, 10, 4, 23, 17]], [[60, 53, 44, 37, 4, 13, 20, 29], [3, 14, 19, 30, 59, 54, 43, 38], [58, 55, 42, 39, 2, 15, 18, 31], [1, 16, 17, 32, 57, 56, 41, 40], [61, 52, 45, 36, 5, 12, 21, 28], [6, 11, 22, 27, 62, 51, 46, 35], [63, 50, 47, 34, 7, 10, 23, 26], [8, 9, 24, 25, 64, 49, 48, 33]], [[35, 26, 17, 1, 62, 53, 44], [46, 37, 21, 12, 3, 64, 55], [57, 41, 32, 23, 14, 5, 66], [61, 52, 43, 34, 25, 16, 7], [2, 63, 54, 45, 36, 27, 11], [13, 4, 65, 56, 47, 31, 22], [24, 15, 6, 67, 51, 42, 33]], [[1, 35, 4, 33, 32, 6], [25, 11, 9, 28, 8, 30], [24, 14, 18, 16, 17, 22], [13, 23, 19, 21, 20, 15], [12, 26, 27, 10, 29, 7], [36, 2, 34, 3, 5, 31]], [[16, 14, 7, 30, 23], [24, 17, 10, 8, 31], [32, 25, 18, 11, 4], [5, 28, 26, 19, 12], [13, 6, 29, 22, 20]], [[1, 14, 4, 15], [8, 11, 5, 10], [13, 2, 16, 3], [12, 7, 9, 6]], [[8, 1, 6], [3, 5, 7], [4, 9, 2]] ] for magic_square in magic_squares: print(DIVIDER_DASH_LINE) if is_magic_square(magic_square) is True: print(f'{GREEN_APPLE} "{magic_square}" is a magic square.') else: print(f'{RED_APPLE} "{magic_square}" is not a magic square.') 

Output

-------------------------------------------------- 🍏 "[[4, 3, 8], [9, 5, 1], [2, 7, 6]]" is a magic square. -------------------------------------------------- 🍏 "[[9, 3, 22, 16, 15], [2, 21, 20, 14, 8], [25, 19, 13, 7, 1], [18, 12, 6, 5, 24], [11, 10, 4, 23, 17]]" is a magic square. -------------------------------------------------- 🍏 "[[60, 53, 44, 37, 4, 13, 20, 29], [3, 14, 19, 30, 59, 54, 43, 38], [58, 55, 42, 39, 2, 15, 18, 31], [1, 16, 17, 32, 57, 56, 41, 40], [61, 52, 45, 36, 5, 12, 21, 28], [6, 11, 22, 27, 62, 51, 46, 35], [63, 50, 47, 34, 7, 10, 23, 26], [8, 9, 24, 25, 64, 49, 48, 33]]" is a magic square. -------------------------------------------------- 🍎 "[[35, 26, 17, 1, 62, 53, 44], [46, 37, 21, 12, 3, 64, 55], [57, 41, 32, 23, 14, 5, 66], [61, 52, 43, 34, 25, 16, 7], [2, 63, 54, 45, 36, 27, 11], [13, 4, 65, 56, 47, 31, 22], [24, 15, 6, 67, 51, 42, 33]]" is not a magic square. -------------------------------------------------- 🍏 "[[1, 35, 4, 33, 32, 6], [25, 11, 9, 28, 8, 30], [24, 14, 18, 16, 17, 22], [13, 23, 19, 21, 20, 15], [12, 26, 27, 10, 29, 7], [36, 2, 34, 3, 5, 31]]" is a magic square. -------------------------------------------------- 🍎 "[[16, 14, 7, 30, 23], [24, 17, 10, 8, 31], [32, 25, 18, 11, 4], [5, 28, 26, 19, 12], [13, 6, 29, 22, 20]]" is not a magic square. -------------------------------------------------- 🍏 "[[1, 14, 4, 15], [8, 11, 5, 10], [13, 2, 16, 3], [12, 7, 9, 6]]" is a magic square. -------------------------------------------------- 🍏 "[[8, 1, 6], [3, 5, 7], [4, 9, 2]]" is a magic square. 

Source

• Magic Square - Wiki

Answer 1

I normally don't like to do complete rewrites for reviews as I don't think that they're usually helpful. Here though, the major problem that I see with your code is you're trying to do far too much "manually". You aren't making good use of built-in Python constructs that automate some of the painful elements. You also have everything in one massive block. I rewrote this from scratch to show how I'd approach the problem fresh.

There are a few discrete problems to solve here:

• Check that each sums correctly:

  • Rows
  • Columns
  • Diagonals

• Check that the square is in fact a square.

• Check that it contains the correct set of numbers.

I see each of these as distinct problems that should be handled separately. In your current code, you have everything mixed together in one massive function which makes it difficult to tell what is responsible for what job. It's simply not very easy code to read.

I ended up breaking the problem up into multiple tiny functions, then tying everything together in is_magic_square:

from typing import List, Iterable, Callable from functools import partial Grid = List[List[int]] # Might as well create an alias for this def has_correct_dimensions(grid: Grid) -> bool: """Returns whether or not the grid is a non-jagged square.""" return all(len(row) == len(grid) for row in grid) def is_normal_square(grid: Grid) -> bool: """Returns whether or not the function contains unique numbers from 1 to n**2.""" max_n = len(grid[0]) ** 2 # Does the set of numbers in the flattened grid contain the same numbers as a range set from 1 to n**2? return set(e for row in grid for e in row) == set(range(1, max_n + 1)) def check_each(iterable: Iterable[Iterable[int]], magic_sum: int) -> bool: """Returns whether or not every sub-iterable collection sums to the magic sum""" return all(sum(elem) == magic_sum for elem in iterable) def diagonal_of(grid: Grid, y_indexer: Callable[[int], int]) -> Iterable[int]: """Generates a line of elements from the grid. y = y_indexer(x).""" return (grid[y_indexer(x)][x] for x in range(len(grid))) def is_magic_square(grid: Grid) -> bool: """Returns whether or not the supplied grid is a proper normal magic square.""" n_rows = len(grid) magic_sum = n_rows * (n_rows ** 2 + 1) / 2 check = partial(check_each, magic_sum=magic_sum) return is_normal_square(grid) and \ has_correct_dimensions(grid) and \ check(grid) and \ # Rows check(zip(*grid)) and \ # Columns check([diagonal_of(grid, lambda x: x), diagonal_of(grid, lambda x: len(grid) - x - 1)]) 

Notice how I have small functions with well defined jobs. Also note how I'm making fairly extensive use of high-level Python helpers. all is great whenever you need to ensure that something is True across over an entire collection. And zip can be used to break the grid into columns.

Even with this all broken up into functions, it's still 7 lines shorter than the original. It's also ~10x faster which I certainly didn't expect since I'm doing expensive shortcut stuff like set(e for row in grid for e in row) == set(range(1, max_n + 1)).

My solutions is far from perfect though. Like I said above, I'm doing a few things quite wastefully. I'm using a lot of lazy operations (like with generator expressions), and repeatedly putting a whole range into a set over and over.

The return in is_magic_square could probably be broken up too. I think it's fine, but it might make some people gag. It could be cleaned up a bit using all:

return all([is_normal_square(grid), has_correct_dimensions(grid), check(grid), check(zip(*grid)), check([diagonal_of(grid, lambda x: x), diagonal_of(grid, lambda x: len(grid) - x - 1)])]) 

At least that gets rid of the ugly line continuations.

---

The major thing in your code that I will point out though is this atrocity:

except: return False 

I think I've mentioned this before: don't do this. If you need to catch an exception, specify the exception, and keep the try in the narrowest scope necessary.

Why? Because, case and point, when I tried to time your function, timeit was showing that your function was executing one million times in 2 seconds. I was blown away. Then I ran the tests though and saw that your code was returning False for every test. After some quick checking, I realized that I had forgotten to import numpy when I pasted your code.

Your code was returning a valid result even though the required packages for the code to run weren't even imported. Stuff like that will eventually bite you via long, painful debugging sessions. Silencing errors is, in my opinion, literally one of the worst things you can possibly do when programming.

Answer 2

One should almost never use a bare except clause. It should always list the exceptions to be caught.

The code would be easier to read and understand, if it were written in section that each tested one aspect of a magic square. Like, is is a square, does it have all the numbers in sequence, do the rows add up to the magic number, do the columns, do the diagonals. Here is a pure python version:

def is_magic_square(grid: List[List[int]]) -> bool: """Returns a boolean if an input grid is magic square""" grid_length = len(grid) grid_area = grid_length**2 magic_sum = float(grid_length * (grid_length ** 2 + 1) / 2) # check the length of all rows if any(len(row) != grid_length for row in grid): return False # check it has all the numbers in sequence if set(x for row in grid for x in row) != set(range(1, grid_area + 1)): return False # check all the rows add up to the magic_number if any(sum(row) != magic_sum for row in grid): return False # check all the columns add up to the magic_number if any(sum(row[col] for row in grid) != magic_sum for col in range(grid_length)): return False # check each diagonal adds up to the magic_number if (sum(grid[i][i] for i in range(grid_length)) != magic_sum or sum(grid[i][grid_length-i-1] for i in range(grid_length)) != magic_sum ): return False return True 

Your code used numpy, it has many useful functions for this task. So here is an alternative version using numpy:

def is_magic_square2(grid: List[List[int]]) -> bool: """Returns a boolean if an input grid is magic square""" grid_length = len(grid) magic_sum = float(grid_length * (grid_length ** 2 + 1) / 2) # check the length of all rows if any(len(row) != grid_length for row in grid): return False npgrid = np.array(grid) # check it has all ints from 1 to grid_length**2 (inclusive) if len(np.setdiff1d(npgrid, np.arange(1, grid_length**2 + 1))): return False # check all the rows add up to the magic_number if any(np.not_equal(npgrid.sum(axis=0), magic_sum)): return False # check all the columns add up to the magic_number if any(np.not_equal(npgrid.sum(axis=1), magic_sum)): return False # check both diagonals add up to the magic_number if (npgrid.diagonal().sum() != magic_sum or np.fliplr(npgrid).diagonal().sum() != magic_sum): return False return True