How to adjust PlotRange automatically depending on the value of the function?

Question

Consider the following test function:

func[x_] = x^3 Exp[-x^2]; 

In general, it may be an arbitrary function without e.g. extrema.

I want to plot it:

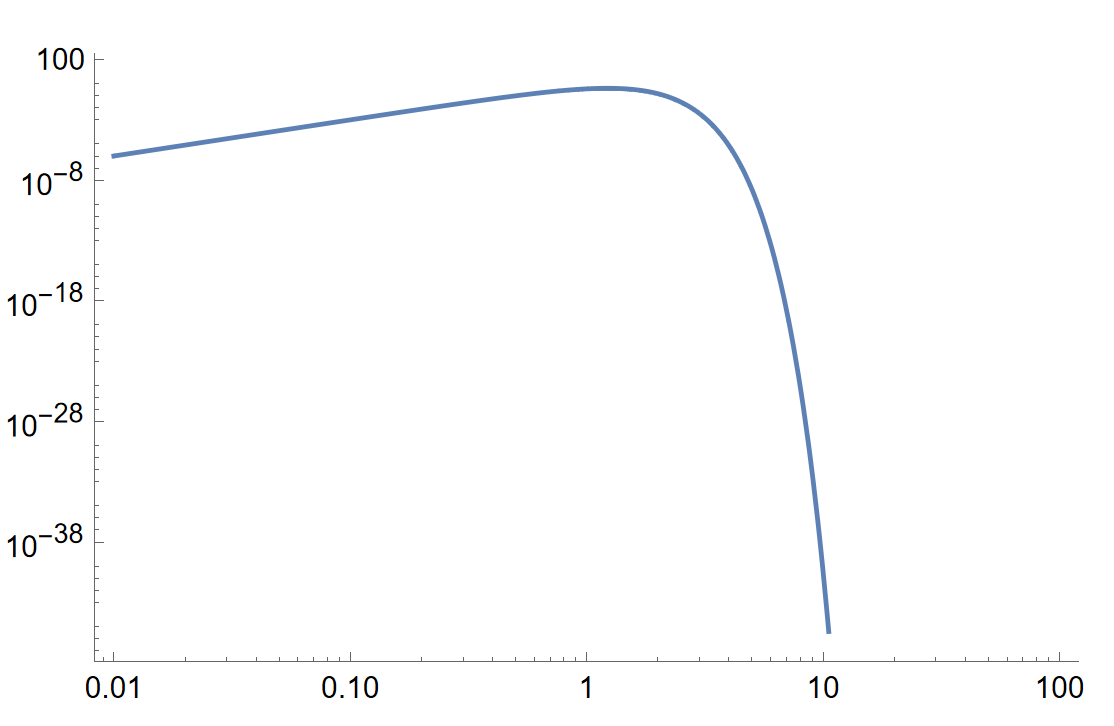
LogLogPlot[func[x], {x, 0.01, 100}] 

Due to the exponential decrease, the automatic PlotRange is down to a very small values.

I want to cut it from below by say 10^-15, but also to adjust the maximal value such that it would correspond to say 1.5*Max[func[x]]. The only thing I know is to use PlotRange:

LogLogPlot[func[x], {x, 0.01, 100}, PlotRange -> {All, {10^-15, 2}}] 

However, the second argument in {10^-15,2} is added by hand. Could you please tell me whether it is possible to make its evaluation automatic depending on the needs?

Answer 1

You could make a function to calculate the vertical bounds of the plot that takes the function as input and calculates the min and max of the function over the range {0.01, 100}. If the min is less than 10^-15, replace it with 10^-15. If you want to calculate the bounds for ranges other than {0.01,100}, you could make those inputs to the function as well:

func[x_] = x^3 Exp[-x^2]; yBounds[f_] := {1.5*MaxValue[{f[x], 0.01 <= x <= 100}, x], Max[MinValue[{f[x], 0.01 <= x <= 100}, x], 10^-15]} LogLogPlot[func[x], {x, 0.01, 100}, PlotRange -> {All, yBounds[func]}]