Quick Sort
Quick Sort is an effective, in-place sorting algorithm that sorts an array using a divide-and-conquer approach. It starts with selecting a pivot element from the array, then partitions the array into two sub-arrays based on whether each of its elements is smaller or larger than the pivot, and finally recursively sorts those sub-arrays.
Quick Sort is widely used in systems where performance and memory efficiency are critical, such as databases, search engines, embedded systems, and high-frequency trading platforms. It also forms the basis for many language-level sorting functions due to its fast average-case performance.
How Quick Sort Works
Here’s a step-by-step explanation of the Quick Sort algorithm:
Step 1: Initial Checks
- If the array is empty or has only one element
low >= high, then it’s already sorted. So, the function returns the array itself.- This is the reason behind not using
data.length == 1as the stopping case for partitioning.
- This is the reason behind not using
Step 2: Partitioning
- Takes the last element’s index
highas the pivot. - Initializes two pointers, i.e.,
leftat the beginninglowandrightat the endhigh - 1(sincehighis the pivot element). - Iterates until
leftandrightmeet or cross.- Moves the pointer
leftto the right when the elements atleftare less than or equal to the pivot. - Moves
rightto the left when the elements atrightare greater than or equal to the pivot.- If both the above conditions are violated and
leftandrighthaven’t crossed, then swaps the numbers at indicesleftandright.
- If both the above conditions are violated and
- Moves the pointer
- If the pointers cross, swaps the pivot with the element at
leftto place the pivot element in its sorted position.
Here is a visual representation for the first iteration:
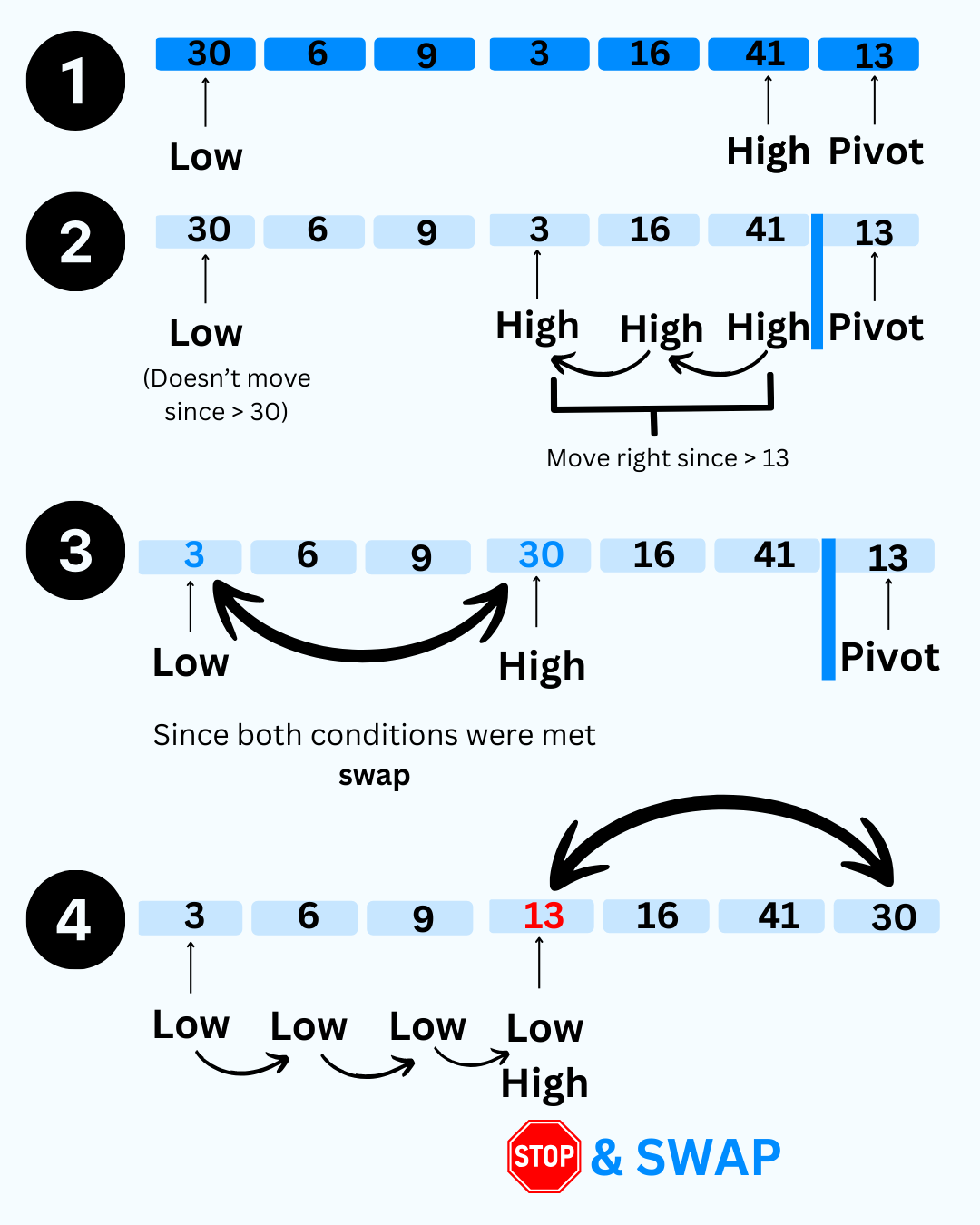
Step 3: Recursive Calls
- Recursively sorts the left subarray (
data[low..left-1]). - Recursively sorts the right subarray (
data[left+1..high]).
Step 4: Helper Function
swap(data, a, b): Swaps elements at indicesaandbin the arraydata.
Implementation of Quick Sort
This example shows an implementation of Quick Sort in Java:
publicclassQuickSortExample{publicstaticvoidquickSort(int[] data,int low,int high){if(low >= high){return;}int left = low;int right = high;int pivot = high;while(left != right){while(data[left]<= data[pivot]&& left < right){left++;}while(data[right]>= data[pivot]&& right > left){right--;}swap(data, left, right);}swap(data, left, pivot);quickSort(data, low, left -1);quickSort(data, left +1, high);}publicstaticvoidswap(int[] data,int a,int b){int temp = data[a];data[a]= data[b];data[b]= temp;}// Example usagepublicstaticvoidmain(String[] args){int[] arr ={34,7,23,32,5,62};System.out.println("Before sorting:");printArray(arr);quickSort(arr,0, arr.length -1);System.out.println("After sorting:");printArray(arr);}publicstaticvoidprintArray(int[] arr){for(int value : arr){System.out.print(value +" ");}System.out.println();}}
In this example, the array arr is sorted using the Quick Sort algorithm.
Here is the output for the example:
Before sorting:34 7 23 32 5 62After sorting:5 7 23 32 34 62
Time Complexity
The efficiency of Quick Sort largely depends on how well the pivot divides the array. Here’s a breakdown of its time complexity in different scenarios:
Best-Case Time Complexity:
The best-case scenario occurs when the pivot element consistently divides the array into two equal halves. This balanced partitioning leads to a logarithmic number of recursive calls, each processing n elements across all levels, resulting in a total time complexity of O(n log n).
Average-Case Time Complexity:
On average, the pivot will not always perfectly split the array, but it generally divides it in a reasonably balanced manner. Even with some imbalance, the number of operations required to partition and sort each level still averages out to O(n log n).
Worst-Case Time Complexity:
The worst-case scenario happens when the pivot consistently ends up being the smallest or largest element, creating highly unbalanced partitions - one of size n - 1 and the other of size 0. This can occur when the given array is already sorted or reverse sorted and the pivot is poorly chosen (e.g., always selecting the first or last element). In such cases, the recursion depth becomes linear (n), and each level requires n comparisons, leading to O(n²) complexity.
Space Complexity
One of the key advantages of Quick Sort is its in-place nature, meaning it does not require additional memory for creating new arrays or lists during the sorting process. Instead, it rearranges elements within the original array, making it highly space-efficient.
The primary space usage comes from the recursive calls. In the best and average cases, where the pivot divides the array fairly evenly, the recursion depth is O(log n), resulting in O(log n) auxiliary space used on the call stack. In the worst-case scenario - such as when the pivot always results in extremely unbalanced partitions (e.g., arrays that are already sorted or reverse sorted with a poor pivot choice) - the recursion depth can grow to O(n). This leads to O(n) space usage on the stack.
Quick Sort vs. Other Sorting Algorithms
This table compares the time and space complexity of Quick Sort with other sorting algorithms:
| Algorithm | Best-Case Time Complexity | Average-Case Time Complexity | Worst-Case Time Complexity | Space Complexity |
|---|---|---|---|---|
| Quick Sort | O(n log n) | O(n log n) | O(n²) | O(log n) |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) | O(n) |
| Heap Sort | O(n log n) | O(n log n) | O(n log n) | O(1) |
| Bubble Sort | O(n) | O(n²) | O(n²) | O(1) |
Frequently Asked Questions
1. Is Quick Sort a stable sorting algorithm?
No, Quick Sort is not stable by default. Stability means that equal elements retain their original order after sorting. However, with modifications, it can be made stable, though this typically sacrifices some performance or simplicity.
2. What is the best way to choose a pivot in Quick Sort?
The choice of pivot significantly affects performance. Common strategies include:
- Picking the middle element
- Using the median-of-three method (first, middle, last)
- Selecting a random element
3. Can Quick Sort be used for linked lists?
While Quick Sort works well for arrays, it’s not ideal for linked lists because of inefficient random access. For linked lists, Merge Sort is generally preferred due to its sequential access and stable nature.
Contribute to Docs
- Learn more about how to get involved.
- Edit this page on GitHub to fix an error or make an improvement.
- Submit feedback to let us know how we can improve Docs.
Learn more on Codecademy
- Career path
Computer Science
Looking for an introduction to the theory behind programming? Master Python while learning data structures, algorithms, and more!Includes 6 CoursesWith Professional CertificationBeginner Friendly75 hours - Free course
Learn Java
Learn to code in Java — a robust programming language used to create software, web and mobile apps, and more.Beginner Friendly17 hours



