Significance
In the last two decades, multiple outbreaks of emerging pathogens have unexpectedly swept the planet. In these public health emergencies, pathogens invade new regions in the span of just a few weeks to months, leaving a critical window of opportunity during which real-time warning could be sounded. As such, accurate prediction of the spatial spread of pathogens could provide invaluable benefits to global public health. Here we develop and validate an operational forecast system that is capable of predicting the spatial transmission of influenza in the United States. In particular, the onset week of local outbreaks can be accurately predicted up to 6 wk in advance at state level.
Keywords: influenza forecast, spatial transmission, data assimilation, human mobility, metapopulation model
Abstract
Recurrent outbreaks of seasonal and pandemic influenza create a need for forecasts of the geographic spread of this pathogen. Although it is well established that the spatial progression of infection is largely attributable to human mobility, difficulty obtaining real-time information on human movement has limited its incorporation into existing infectious disease forecasting techniques. In this study, we develop and validate an ensemble forecast system for predicting the spatiotemporal spread of influenza that uses readily accessible human mobility data and a metapopulation model. In retrospective state-level forecasts for 35 US states, the system accurately predicts local influenza outbreak onset,—i.e., spatial spread, defined as the week that local incidence increases above a baseline threshold—up to 6 wk in advance of this event. In addition, the metapopulation prediction system forecasts influenza outbreak onset, peak timing, and peak intensity more accurately than isolated location-specific forecasts. The proposed framework could be applied to emergent respiratory viruses and, with appropriate modifications, other infectious diseases.
Influenza remains a serious worldwide threat to the public health. For the United States, analyses of historical outbreaks have yielded some understanding of the spatial movement and traveling waves associated with the spread of influenza for both interpandemic (1) and pandemic seasons (2, 3). However, despite the tremendous resources and efforts invested in studying the spread and prediction of influenza (1–19), forecast of the spatial dispersion of this pathogen in real time remains challenging.
Previous studies have shown that a close relationship exists between infectious disease spread and human mobility as measured by both long-distance airline travel and short-distance work-related commuting (1, 4–11). Despite its importance, human movement data more detailed than the coarse-grained data reported in census surveys are currently unavailable in real time. We here develop an operational forecasting system that uses available commuter data to estimate human mobility and predict the spatial–temporal spread of influenza in the United States.
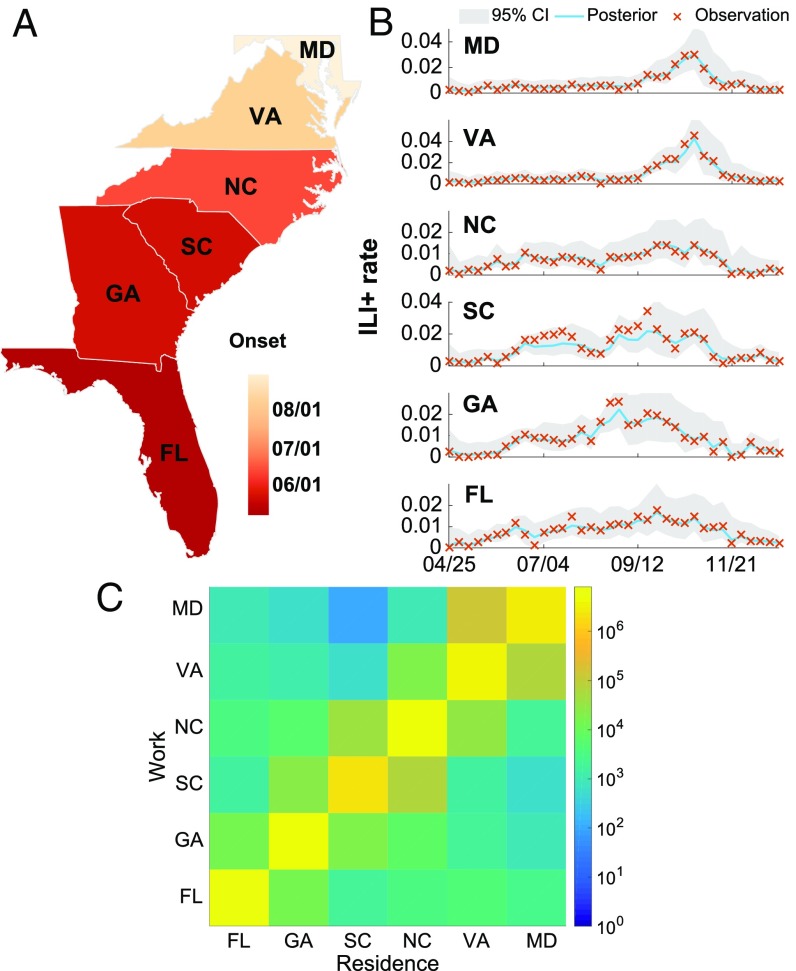
We developed this system using patient syndromic and laboratory data from the US Department of Defense (DOD) Armed Forces Health Surveillance Branch (AFHSB) (Materials and Methods). Local influenza activity is reflected as the percentage of patients with influenza type A among all people seeking medical attention, termed influenza-like illness plus (ILI+) hereafter. ILI is delineated by 29 International Classification of Diseases (ICD-9) codes associated with influenza-like illness (SI Appendix, Table S1), and ILI+ is calculated as the product of weekly ILI and concurrent influenza type A positivity rates (20). In these ILI+ data, we observe the clear spatial movement of influenza during the 2009 pandemic season (Fig. 1 A and B). Consistent with previous empirical studies, the onset of 2009 influenza pandemic in each of six states along the east coast of the United States (Florida, Georgia, South Carolina, North Carolina, Virginia, and Maryland) is found to be lagged from south to north (2), occurring later in the year with increasing distance from the outbreak origin in Mexico (21). We define onset as the first of three consecutive weeks with ILI+ over 0.5%. The apparent spatial diffusion from south to north is evident in the ILI+ curves from these six states. Although the AFHSB data only cover a small fraction of the total US population and may suffer reporting bias issues, it has been previously shown that this dataset agrees well with the activity recorded in US Centers for Disease Control and Prevention (CDC) surveillance data during the 2009 pandemic season (22).
Fig. 1.
The spatial transmission of influenza along the east coast of the United States during the 2009 pandemic season. (A) Onset date in six states: Florida (FL), Georgia (GA), South Carolina (SC), North Carolina (NC), Virginia (VA), and Maryland (MD). (B) Weekly ILI+ rates (cross symbols) for each state. The solid lines and shaded areas are the posterior mean and 95% credible intervals (CI), respectively, of the metapopulation model–EAKF fit. The states are arranged by geographical location from south (bottom) to north (top). (C) Numbers of recurrent commuters between the six states.
Metapopulation Model
To forecast the spatial diffusion of ILI+, we developed a metapopulation model that can flexibly generate patterns of spatial transmission. We used ILI+ resolved at the state level. Within the model, the different states are connected by mobility flows (11), including movement by recurrent commuters and random visitors. The numbers of work commuters crossing state lines are available from the US census survey (23). For example, for the six southeastern US states, most commuting events occur between contiguous states, while long-range movements are quite rare (Fig. 1C and SI Appendix, Analysis of the Commuting Pattern Across States and Fig. S1). Using the commuting data, the total population in states is subdivided into subpopulations , where represents the fixed subpopulation living in state and commuting to work in state . In constructing our metapopulation model, we aim to track the evolution of the susceptible () and infected () population in each , and simulate influenza transmission using a humidity-driven susceptible–infected–recovered–susceptible (SIRS) model (24, 25) (SI Appendix, Humidity-Driven SIRS Model).
Because the population composition in each state differs during day and night time, we separate the transmission equations into two parts. During daytime, subpopulation is present in state and participates in transmission there. The total, susceptible, and infected populations in state during daytime are simply , , and , respectively.
In addition to fixed commuting flows, we also simulate the irregular movement of visitors who travel for reasons other than work: business trips or vacations, for example. These individuals circulate among subpopulations following a Markov process, causing a population exchange in all subpopulations . Transportation records of flights, trains, and buses exist; however, this information is typically released after a long lag period and varies in availability across different locations and data sources. Due to a lack of real-time information on this movement, we assume the number of random visitors traveling from state to is proportional to the average number of commuters between them: . In particular, the random visitors from state to are assumed to be , where is an adjustable parameter. The rationale behind this proportionality assumption is that, if two locations exchange a larger number of commuters, there should exist a stronger economic tie or other incentives to facilitate the exchange of random visitors.
During daytime, persons, drawn uniformly from the population present in state , move to state and are randomly redistributed into the subpopulations there. Such population exchange exists for all pairs of states. This implies that the infected individuals leaving subpopulation are , where is the total number of random visitors leaving state , and is the ratio of the number of infected people from subpopulation to the total population of state . Similarly, the infected individuals entering can be calculated as , where is the total number of infected persons entering state , and is the ratio of subpopulation to the total population of state . The random exchange of susceptible individuals can be calculated similarly. Combining the regular commuters and random visitors, the transmission equations for and during daytime are
| [1] |
| [2] |
Here is the contact rate at time at state , is the duration of infection, and is the duration of immunity. The transmission equations at nighttime are formulated similarly (SI Appendix, Metapopulation Model). During implementation, we assume daytime and nighttime transmissions last for 8 and 16 h, respectively. That is, the model is integrated deterministically using the daytime equations for an interval of 1/3 d, and then the nighttime equations are integrated for the subsequent 2/3 d. The number of new infections in subpopulation is calculated using the contact terms determined through model integration. Observations at location , i.e., weekly incidence, are obtained by summing the new infections in subpopulations whose living location is .
Parameter Inference
The metapopulation model is capable of generating abundant scenarios of spatial spread from variable ratios of work commuters and random visitors by adjusting the parameter . This relatively parsimonious construct allows its application in conjunction with statistical filtering techniques, which, in combination, can be used to infer model state space and parameters and to generate ensemble forecasts (SI Appendix, Model–Data Assimilation Framework).
Similar model–data assimilation frameworks have been successfully used to forecast the local epidemic trajectory for a number of infectious diseases (13–16, 26). During model training, the state variables and parameters in the dynamical model are repeatedly calibrated by available observations; a forecast is then generated by integrating the optimized model into the future. In practice, an ensemble of randomly generated epidemic trajectories is simulated to produce a probabilistic distribution of forecast outcomes.
The metapopulation model possesses a high-dimensional state vector. For each subpopulation , we record three variables: , , and weekly incidence. The parameters (the maximal basic reproductive number), (the minimal basic reproductive number), (duration of immunity), (length of infectious period), and (random movement ratio) are shared for all subpopulations. For metapopulation forecasts at a high geographical resolution, the dimension of state vectors will undergo a quadratic growth as the number of locations increases. To deal with this high-dimensional data assimilation problem, we chose an efficient filtering algorithm: the Ensemble Adjustment Kalman Filter (EAKF) (31). Unlike particle filters (32), which require a larger number of particles for high-dimensional problems and are more suitable for low-dimension systems (33), the EAKF uses a limited number of ensemble members and is conducive for use with high-dimension systems. Previous forecast work has shown that the performances of particle filters and the EAKF are similar when used to produce influenza forecasts in conjunction with a SIRS model (13). In Fig. 1B, the posterior fitting of the metapopulation model–EAKF to the southeastern US states during the 2009 pandemic is presented. The epidemic curves are well captured by the model–data assimilation system.
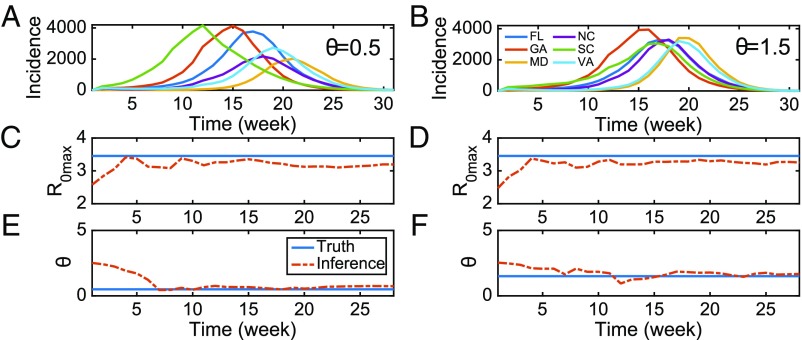
To validate the forecast system further, we next examined whether key model parameters can be accurately recovered from model-generated synthetic outbreaks with known true values (i.e., the “truth”). Two such outbreaks were generated using the metapopulation model for the six southeastern US states and the same initial conditions and parameters excepting a change of parameter (Fig. 2 A and B). To mimic observational error, we added noise to the model-generated time series of influenza incidence. The prescribed observational error variance, OEV, at week is defined as . We then used the metapopulation model–EAKF framework, in conjunction with these error-laden observations, to estimate the model parameters. In Fig. 2 C–F, we report the posterior mean of two of the more sensitive parameters, (the maximal basic reproductive number) and (the random movement ratio), as inferred by the metapopulation model–EAKF system. For both outbreak simulations, the metapopulation model estimates of these parameters, inferred using observations from all six states, are rapidly adjusted toward the truth. Additional analyses indicate that inference accuracy is not particularly sensitive to the initial conditions of the model (SI Appendix, Inference of Parameters and Variables and Figs. S2–S4). Further, the metapopulation forecast system generates more-accurate forecasts of onset week, peak timing, and peak intensity for the synthetic truth, compared with a reference SIRS–EAKF system in which each state is modeled in isolation (13, 14) (SI Appendix, Forecasts of Synthetic Outbreaks and Fig. S5).
Fig. 2.
Inference of key parameters in the metapopulation model. (A and B) Weekly incidence of new infections generated by the metapopulation model for six states (FL, GA, MD, NC, SC, and VA). Both simulations were generated with the same initial conditions, except for (A) and (B) . Epidemic curves for different states are distinguished with distinct colors. (C; and D) Inference of (the maximal basic reproductive number) using the metapopulation model–EAKF system. The solid blue line indicates the true parameter used in synthetic outbreaks, and the red dashed line represents the posterior mean during data assimilation. (E; and F) Inference of the parameter (random movement ratio) in the metapopulation system.
In these synthetic tests, the metapopulation model was run deterministically. For infectious diseases for which only sporadic case numbers are observed, a deterministic model could introduce significant errors by rounding the real number estimates of infection cases to integer values, and a stochastic model may be preferable; however, the deterministic model is suitable in this study of seasonal influenza, as large numbers of infections exist. Indeed, we also ran a stochastic version of the metapopulation model in synthetic tests and found no significant change in forecast accuracy (SI Appendix, Fig. S6).
Retrospective Forecasts
We next performed retrospective forecasts for 35 states in the continental United States for the 2008–2009 through 2012–2013 influenza seasons, using the AFHSB type A ILI+ data. The remaining 15 states were excluded, as they were not well represented in the AFHSB dataset due to low numbers of ILI records (SI Appendix, Fig. S7). The remaining AFHSB ILI+ data provide reasonable time series representations of influenza incidence at national and state levels (Fig. 3A and SI Appendix, Fig. S8). We also performed synthetic tests using the full 35-state system, which showed that key parameters, such as and , can still be accurately inferred (SI Appendix, Fig. S9).
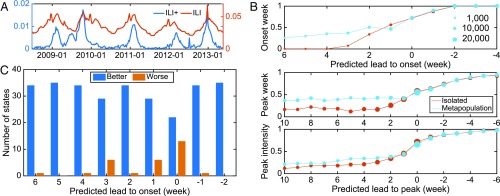
Fig. 3.
Forecasting the spatial transmission of type A influenza in the United States. (A) ILI+ (blue color) and ILI (red color) curves at the national level. (B) Average forecast accuracy of onset week, peak week, and peak intensity for both metapopulation and isolated forecasts, across 35 states and five seasons. The y axis scale indicates the fraction of accurate predictions within each group. Symbol size reflects the total number of forecasts in each group in a linear scale. (C) Performance of the metapopulation forecasts by onset week prediction compared with the isolated forecasts in individual states. The blue (orange) bars indicate the number of states where the metapopulation forecast is better (worse).
For each season, we generated 100 independent ensemble forecasts for each week during the flu season using both the metapopulation model and the isolated SIRS model (SI Appendix, Retrospective Forecasts of Historical Outbreaks and Figs. S10–S12). As the actual onset and peak weeks are unknown in real time, we evaluated forecast accuracy relative to the predicted onset or peak week. Specifically, forecast accuracy for onset and peak week (peak intensity) is the fraction of ensemble mean predictions within 1 wk (25%) from the observed. Fig. 3B shows average forecast accuracy for onset week, peak week, and peak intensity over all seasons and states. Here, a positive predicted lead indicates that onset or peak week is predicted to occur in the future, while a negative value implies that the onset or peak week is predicted to have already passed. Onset week was predicted up to 6 wk in advance by the metapopulation system, whereas the isolated forecasts failed to predict most onset events until a predicted lead of 2 wk. In Fig. 3C, we summarize the performance of the metapopulation forecasts of onset week compared with the isolated forecasts for the individual states. Onset predictions for a few states were degraded (particularly at shorter leads); however, the majority of states had improved onset forecast accuracy with the metapopulation model. Sensitivity analysis showed that this improvement held for alternate definitions of onset (SI Appendix, Fig. S13). In addition, the metapopulation forecast system was more accurate in predicting the peak week and peak intensity for all prospective forecasts (i.e., lead > 0 wk). Forecast accuracy improvement for onset week, peak week, and peak intensity is summarized in Table 1. All improvements were found to be statistically significant. In particular, the improvements for onset week and peak week are more pronounced, up to 35% and 31%, respectively, several weeks before onset/peak. For peak intensity, which is a more challenging forecast target, the metapopulation forecasts still outperformed the isolated predictions, albeit to a lesser extent.
Table 1.
Accuracy improvement of the metapopulation forecasts over isolated forecasts for onset week, peak week, and peak intensity
| Predicted lead to event, % | |||||
| Target | 6 wk | 5 wk | 4 wk | 3 wk | 2 wk |
| Onset week | |||||
| Peak week | |||||
| Peak intensity | |||||
Asterisks indicate the statistical significance obtained from bootstrap analysis: 0.01<*P <0.05; **P <10−5.
Our results indicate that the benefits of using a metapopulation system to predict onset are two-fold: (i) The number of state-season instances where an onset was predicted (as opposed to a forecast of no onset) was larger with the metapopulation system (SI Appendix, Table S2), and (ii) for instances where both the metapopulation and isolated systems predicted onset, the metapopulation system was more often correct.
To further validate the effectiveness of the proposed forecast framework, we applied it to a smaller geographical scale at the county level. In particular, seven contiguous counties in southeast Virginia with sufficient AFHSB ILI+ data were selected. Similar improvements were observed at the county level and are reported (SI Appendix, Retrospective Forecasts at the County Level and Fig. S14).
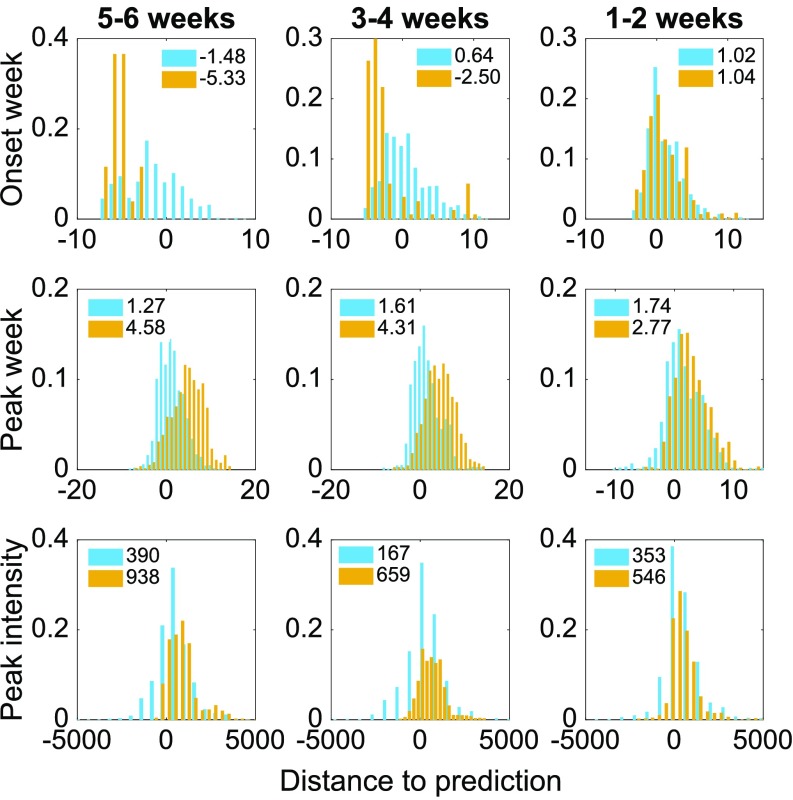
The above validation metrics are defined based on observations. However, these observations in real-world surveillance systems intrinsically contain a certain level of stochasticity. Another approach to validating the forecast system is to regard each observation as a single realization of a stochastic process. From this point of view, we can explore how the observations distribute with respect to the predicted values. If the forecasts are providing a good estimate of the truth, the observations, i.e., single realizations of a stochastic process, should be normally distributed around the predictions with zero mean, that is, an accurate forecast. If, on the other hand, the mean error is nonzero, there remains bias/inaccuracy in the prediction. By looking at the scatter of observations around many predictions, we can obtain an estimate of that inaccuracy. In Fig. 4, we show the distributions of the distance of the observations (onset week, peak week, and peak intensity) from predicted values across all 35 states and five seasons. In particular, we first grouped the forecasts according to their predicted lead to onset (peak) for onset week (peak week and peak intensity) predictions from 6 wk to 1 wk, and then plotted the distribution of the discrepancy of observations from corresponding predictions within each category, for both metapopulation and isolated predictions.
Fig. 4.
Distributions of the distance from the observed targets to the predicted values. The blue bars represent metapopulation forecasts; the orange ones represent the isolated forecasts. The mean bias of each distribution is displayed in the legend of each subplot. (Top) For onset forecasts with predicted leads of 5 to 6, 3 to 4, and 1 to 2 wk, the distributions of the observed onset week with respect to the predicted values (x axis is the value of observed onset week minus predicted onset week) across all 35 states and five seasons are displayed, for both the metapopulation and isolated forecasts. (Middle and Bottom) Same analysis for (Middle) peak week and (Bottom) peak intensity, grouped by the predicted lead to peak. The x axis for Bottom is the value of observed peak intensity (incidence per 100,000 people) minus predicted peak intensity.
Unlike the metapopulation forecast system, the isolated forecast appears more sensitive to observation noise. For onset week, low incidence produces no-onset predictions due to a lack of signal, whereas, for the metapopulation model, early incidence signal is picked up from neighboring localities and inferred random movement levels. In addition, for the isolated forecasts predicting an onset, initial low-incidence weeks can drive the forecast system to erroneously predict a late onset, as indicated by the negative bias in onset predictions (Fig. 4, Top). For peak week, the isolated forecast tends to predict an outbreak peak too early in the future, and fails to capture the growing trend during low-incidence weeks (the positive bias observed in Fig. 4, Middle). For peak intensity, the isolated forecast trajectories tend to undershoot observed incidence (SI Appendix, Fig. S15B), which produces a positive bias in peak intensity prediction (Fig. 4, Bottom). These biases in the isolated forecasts are substantially reduced by the metapopulation forecast for all three targets.
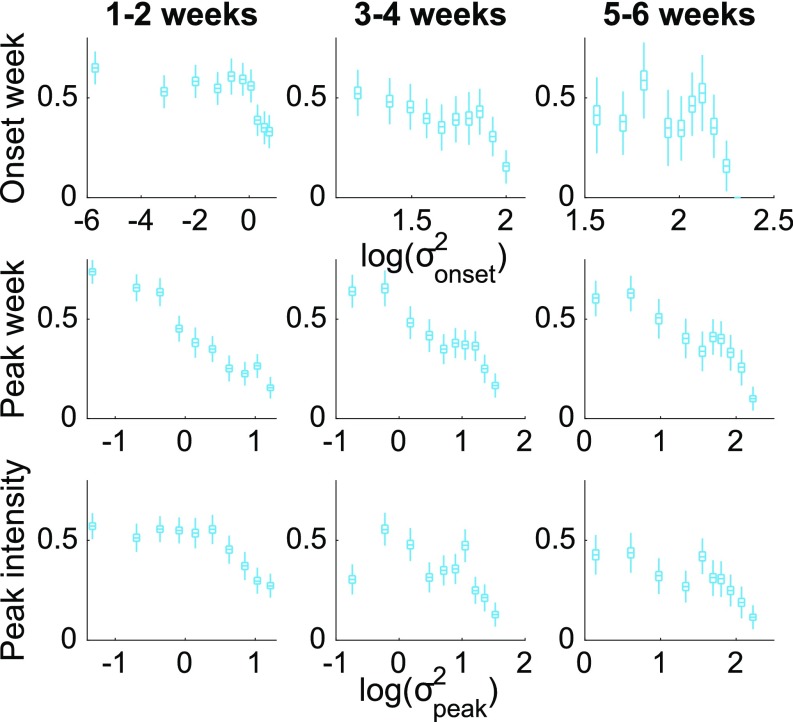
The accuracy of onset week predictions can be further discriminated by the spread of the ensemble forecasts (13, 14). Metapopulation forecasts for the five seasons and 35 states were grouped into three categories according to their predicted onset lead (i.e., how far in the future onset is forecast to occur). Within each lead category, we plot forecast accuracy as a function of the ensemble variance of predicted onset log transformed, , a measure of the within-ensemble spread of predictions (Fig. 5, Top). Forecasts with a smaller ensemble spread are found to be more reliable. This also holds for peak week and peak intensity, calibrated by the ensemble predicted peak variance log transformed, (Fig. 5, Middle and Bottom). This finding indicates that the likelihood a particular metapopulation model forecast is accurate can be estimated in real time.
Fig. 5.
Forecast accuracy calibrated by the ensemble variance. (Top) For each group of onset forecasts with predicted leads of 1 to 2, 3 to 4, and 5 to 6 wk, forecast accuracy is plotted as a function of the ensemble predicted onset variance log transformed, . Forecasts in each group are divided into 10 data bins with same number of forecasts. Box plots indicate bootstrap confidence intervals [box, interquartile (IQR, Q1 to Q3); whisker, Q1 to Q1 - 1.5 IQR and Q3 to Q3 + 1.5 IQR] obtained with bootstrap resampling of the forecasts (SI Appendix, Bootstrap Confidence Interval). (Middle and Bottom) Same analysis for (Middle) peak week and (Bottom) peak intensity, but grouped by the predicted lead to peak and calibrated by the ensemble predicted peak variance log transformed, .
Discussions
In this work, we have developed and validated an operational forecast system that can successfully predict the spatial transmission of influenza in the United States at both the state and county levels. By assimilating surveillance data from multiple locations, forecast accuracy for onset week, peak week, and peak intensity is enhanced by the metapopulation forecast system up to 35%, 31%, and 13%, respectively, compared with baseline forecasts made at each location in isolation. The proposed framework is flexible because its implementation is independent of specific disease transmission dynamics. As a result, it has potential to be adapted for use in the forecast of other infectious diseases.
The last few decades have witnessed the rapid emergence and worldwide spread of multiple novel infectious diseases, including severe acute respiratory syndrome, Middle East respiratory syndrome, Zika, Chikungunya, Ebola, H5N1 avian influenza, and 2009 pandemic H1N1 influenza. In an increasingly interconnected world, accurate forecast of the spatial progression of infectious disease can provide useful evidence-based information for policy-making and containment coordination. The forecast system presented here, which combines an intermediate-complexity metapopulation model, an efficient data assimilation technique, publicly available commuting and humidity data, and state-level surveillance data, can be run operationally in real time to generate predictions of future disease incidence and spread.
In the upcoming 2017–2018 season, the CDC will launch a real-time ILI forecast challenge for participating US teams (34). The proposed framework will be tested and evaluated in real time for this challenge. We will also incorporate the metapopulation framework into the real-time forecasts of ILI+ we generate and publish at state and municipal scales (35). These real-time efforts will facilitate the transformation of infectious disease forecasting from research to routine operation and its integration into decision-making.
Materials and Methods
Data Description.
The patient syndromic and laboratory test data were obtained from the US DOD AFHSB. The syndromic data contain patient line records from 58,520,410 visits, to permanent military treatment facilities (MTFs), attributed to influenza-like illness (ILI), as delineated by 29 ICD-9 codes associated with ILI (SI Appendix, Table S1). The ILI-related visit records span a period of over 13 y, from January 1, 2000 to May 31, 2013, and cover ∼1,000 MTFs located in 42 states in the United States, whose locations are identified with their associated zip codes. Patients include both military personnel and other beneficiaries (spouses and children). Using the weekly total visit number for any reason at each MTF, we can normalize the weekly ILI-related visits in each state to calculate the ILI rate.
The laboratory data provide the results of influenza type A and type B tests performed for 464,108 patients during October 1, 2006 to September 24, 2013. We focused on influenza type A in our analysis because type A accounts for a larger proportion of confirmed influenza (type A, 53,067 cases; type B, 11,733 cases). The weekly ILI+ rate in each state was then calculated as the product of the weekly ILI rate and concurrent weekly influenza type A positivity rate. Compared with ILI, ILI+ provides a clearer signal of influenza type A activity (20). To ensure sufficient sample size in the surveillance data, we selected, for retrospective forecasting, the 35 states that each documented more than 30,000 total ILI-related visits (SI Appendix, Fig. S7). In addition, because the laboratory test numbers during 2006 and 2007 were relatively small, we chose to restrict retrospective forecasting to the five consecutive flu seasons from 2008 to 2013.
County-to-county commute data were obtained from the 2009–2013 American Community Surveys, which are publicly available from the website of the United States Census Bureau (23). The data contain both the estimated commuting population between counties and the 90% confidence interval of the estimation. For the retrospective forecasts of 35 states, we transformed the county-level commute data to state level by only considering cross-state commuting. As our forecast seasons (2008–2013) largely overlap with the survey period, we assume the commute data are representative of our study period.
Absolute humidity (AH) conditions for each state are local daily climatological humidity data averaged over a 24-y period (1979–2002) and derived from North American Land Data Assimilation System data (36).
Data Availability.
The AH data and commute data are deposited at figshare (https://doi.org/10.6084/m9.figshare.5687503.v1). The county-to-county commute data are available online at https://www.census.gov/topics/employment/commuting.html.
Supplementary Material
Acknowledgments
The research is supported by US National Institutes of Health (NIH) Grants GM110748, GM100467, and ES009089, and Contract HDTRA1-15-C-0018 from the Defense Threat Reduction Agency. We thank the US DOD AFHSB for providing the surveillance data. The opinions stated are those of the authors and do not represent the official position of the NIH or DOD.
Footnotes
Conflict of interest statement: J.S. discloses partial ownership of SK Analytics. S.P., S.K., and W.Y. disclose consultation for SK Analytics.
This article is a PNAS Direct Submission.
Data deposition: The absolute humidity data and state-level commute data have been deposited to Figshare, available at https://dx.doi.org/10.6084/m9.figshare.5687503.v1. The county-to-county commute data are available online at https://www.census.gov/topics/employment/commuting.html.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1708856115/-/DCSupplemental.
References
- 1.Viboud C, et al. Synchrony, waves, and spatial hierarchies in the spread of influenza. Science. 2006;312:447–451. doi: 10.1126/science.1125237. [DOI] [PubMed] [Google Scholar]
- 2.Gog JR, et al. Spatial transmission of 2009 pandemic influenza in the US. PLoS Comput Biol. 2014;10:e1003635. doi: 10.1371/journal.pcbi.1003635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Charu V, et al. Human mobility and the spatial transmission of influenza in the United States. PLoS Comput Biol. 2017;13:e1005382. doi: 10.1371/journal.pcbi.1005382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Colizza V, Barrat A, Barthélemy M, Vespignani A. The role of the airline transportation network in the prediction and predictability of global epidemics. Proc Natl Acad Sci USA. 2006;103:2015–2020. doi: 10.1073/pnas.0510525103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Balcan D, et al. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc Natl Acad Sci USA. 2009;106:21484–21489. doi: 10.1073/pnas.0906910106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Balcan D, Vespignani A. Phase transitions in contagion processes mediated by recurrent mobility patterns. Nat Phys. 2011;7:581–586. doi: 10.1038/nphys1944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brockmann D, Helbing D. The hidden geometry of complex, network-driven contagion phenomena. Science. 2013;342:1337–1342. doi: 10.1126/science.1245200. [DOI] [PubMed] [Google Scholar]
- 8.Riley S. Large-scale spatial-transmission models of infectious disease. Science. 2007;316:1298–1301. doi: 10.1126/science.1134695. [DOI] [PubMed] [Google Scholar]
- 9.Keeling MJ, Rohani P. Estimating spatial coupling in epidemiological systems: A mechanistic approach. Ecol Lett. 2002;5:20–29. [Google Scholar]
- 10.Keeling MJ, Danon L, Vernon MC, House TA. Individual identity and movement networks for disease metapopulations. Proc Natl Acad Sci USA. 2010;107:8866–8870. doi: 10.1073/pnas.1000416107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Belik V, Geisel T, Brockmann D. Natural human mobility patterns and spatial spread of infectious diseases. Phys Rev X. 2011;1:011001. [Google Scholar]
- 12.Ginsberg J, et al. Detecting influenza epidemics using search engine query data. Nature. 2009;457:1012–1014. doi: 10.1038/nature07634. [DOI] [PubMed] [Google Scholar]
- 13.Shaman J, Karspeck A. Forecasting seasonal outbreaks of influenza. Proc Natl Acad Sci USA. 2012;109:20425–20430. doi: 10.1073/pnas.1208772109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shaman J, Karspeck A, Yang W, Tamerius J, Lipsitch M. Real-time influenza forecasts during the 2012-2013 season. Nat Comm. 2013;4:2837. doi: 10.1038/ncomms3837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yang W, Olson DR, Shaman J. Forecasting influenza outbreaks in boroughs and neighborhoods of New York City. PLoS Comput Biol. 2016;12:e1005201. doi: 10.1371/journal.pcbi.1005201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pei S, Shaman J. Counteracting structural errors in ensemble forecast of influenza outbreaks. Nat Comm. 2017;8:925. doi: 10.1038/s41467-017-01033-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tizzoni M, et al. Real-time numerical forecast of global epidemic spreading: Case study of 2009 A/H1N1pdm. BMC Med. 2012;10:165. doi: 10.1186/1741-7015-10-165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Farrow DC, et al. A human judgment approach to epidemiological forecasting. Plos Comput Biol. 2017;13:e1005248. doi: 10.1371/journal.pcbi.1005248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Biggerstaff M, et al. Results from the centers for disease control and prevention’s predict the 2013-2014 Influenza Season Challenge. BMC Infect Dis. 2016;16:357. doi: 10.1186/s12879-016-1669-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Goldstein E, Viboud C, Charu V, Lipsitch M. Improving the estimation of influenza-related mortality over a seasonal baseline. Epidemiology. 2012;23:829–838. doi: 10.1097/EDE.0b013e31826c2dda. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fraser C, et al. Pandemic potential of a strain of influenza A (H1N1): Early findings. Science. 2009;324:1557–1561. doi: 10.1126/science.1176062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Riley P, et al. Multiple estimates of transmissibility for the 2009 influenza pandemic based on influenza-like-illness data from small US military populations. Plos Comput Biol. 2013;9:e1003064. doi: 10.1371/journal.pcbi.1003064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.United States Census Bureau 2013 County to county commuting data. Available at https://www.census.gov/topics/employment/commuting.html. Accessed November 15, 2016.
- 24.Shaman J, Pitzer VE, Viboud C, Grenfell BT, Lipsitch M. Absolute humidity and the seasonal onset of influenza in the continental United States. Plos Biol. 2010;8:e1000316. doi: 10.1371/journal.pbio.1000316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shaman J, Kohn M. Absolute humidity modulates influenza survival, transmission, and seasonality. Proc Natl Acad Sci USA. 2009;106:3243–3248. doi: 10.1073/pnas.0806852106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.DeFelice NB, Little E, Campbell SR, Shaman J. Ensemble forecast of human West Nile virus cases and mosquito infection rates. Nat Commun. 2017;8:14592. doi: 10.1038/ncomms14592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Reis J, Shaman J. Retrospective parameter estimation and forecast of respiratory syncytial virus in the United States. PLoS Comput Biol. 2016;12:e1005133. doi: 10.1371/journal.pcbi.1005133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yang W, et al. Transmission network of the 2014-2015 Ebola epidemic in Sierra Leone. J R Soc Interface. 2015;12:20150536. doi: 10.1098/rsif.2015.0536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yamana T, Kandula S, Shaman J. Superensemble forecasts of dengue outbreaks. J R Soc Interface. 2016;13:20160410. doi: 10.1098/rsif.2016.0410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yang W, Karspeck A, Shaman J. Comparison of filtering methods for the modeling and retrospective forecasting of influenza epidemics. Plos Comput Biol. 2014;10:e1003583. doi: 10.1371/journal.pcbi.1003583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Anderson JL. An ensemble adjustment Kalman filter for data assimilation. Mon Weather Rev. 2001;129:2884–2093. [Google Scholar]
- 32.Arulampalam MS, Maskell S, Gordon N, Clapp T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans Signal Process. 2002;50:174–188. [Google Scholar]
- 33.Snyder C, Bengtsson T, Bickel P, Anderson J. Obstacles to high-dimensional particle filtering. Mon Weather Rev. 2008;136:4629–4640. [Google Scholar]
- 34.United States Centers for Disease Control and Prevention 2017 Epidemic Prediction Initiative. Available at https://predict.phiresearchlab.org/. Accessed November 15, 2016.
- 35.Columbia Prediction of Infectious Diseases Available at https://cpid.iri.columbia.edu. Accessed November 15, 2016.
- 36.Cosgrove BA, et al. Real-time and retrospective forcing in the North American Land Data Assimilation System (NLDAS) project. J Geophys Res. 2003;108:8842. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The AH data and commute data are deposited at figshare (https://doi.org/10.6084/m9.figshare.5687503.v1). The county-to-county commute data are available online at https://www.census.gov/topics/employment/commuting.html.