Given a string s, return the longest palindromic substring in s.
Example 1:
Input: s = "babad" Output: "bab" Note: "aba" is also a valid answer. Example 2:
Input: s = "cbbd" Output: "bb" Example 3:
Input: s = "a" Output: "a" Example 4:
Input: s = "ac" Output: "a" Constraints:
1 <= s.length <= 1000sconsist of only digits and English letters (lower-case and/or upper-case),
给你一个字符串 s,找到 s 中最长的回文子串。
此题非常经典,并且有多种解法。
解法一,动态规划。定义
dp[i][j]表示从字符串第i个字符到第j个字符这一段子串是否是回文串。由回文串的性质可以得知,回文串去掉一头一尾相同的字符以后,剩下的还是回文串。所以状态转移方程是dp[i][j] = (s[i] == s[j]) && ((j-i < 3) || dp[i+1][j-1]),注意特殊的情况,j - i == 1的时候,即只有 2 个字符的情况,只需要判断这 2 个字符是否相同即可。j - i == 2的时候,即只有 3 个字符的情况,只需要判断除去中心以外对称的 2 个字符是否相等。每次循环动态维护保存最长回文串即可。时间复杂度 O(n^2),空间复杂度 O(n^2)。解法二,中心扩散法。动态规划的方法中,我们将任意起始,终止范围内的字符串都判断了一遍。其实没有这个必要,如果不是最长回文串,无需判断并保存结果。所以动态规划的方法在空间复杂度上还有优化空间。判断回文有一个核心问题是找到“轴心”。如果长度是偶数,那么轴心是中心虚拟的,如果长度是奇数,那么轴心正好是正中心的那个字母。中心扩散法的思想是枚举每个轴心的位置。然后做两次假设,假设最长回文串是偶数,那么以虚拟中心往 2 边扩散;假设最长回文串是奇数,那么以正中心的字符往 2 边扩散。扩散的过程就是对称判断两边字符是否相等的过程。这个方法时间复杂度和动态规划是一样的,但是空间复杂度降低了。时间复杂度 O(n^2),空间复杂度 O(1)。
解法三,滑动窗口。这个写法其实就是中心扩散法变了一个写法。中心扩散是依次枚举每一个轴心。滑动窗口的方法稍微优化了一点,有些轴心两边字符不相等,下次就不会枚举这些不可能形成回文子串的轴心了。不过这点优化并没有优化时间复杂度,时间复杂度 O(n^2),空间复杂度 O(1)。
解法四,马拉车算法。这个算法是本题的最优解,也是最复杂的解法。时间复杂度 O(n),空间复杂度 O(n)。中心扩散法有 2 处有重复判断,第一处是每次都往两边扩散,不同中心扩散多次,实际上有很多重复判断的字符,能否不重复判断?第二处,中心能否跳跃选择,不是每次都枚举,是否可以利用前一次的信息,跳跃选择下一次的中心?马拉车算法针对重复判断的问题做了优化,增加了一个辅助数组,将时间复杂度从 O(n^2) 优化到了 O(n),空间换了时间,空间复杂度增加到 O(n)。
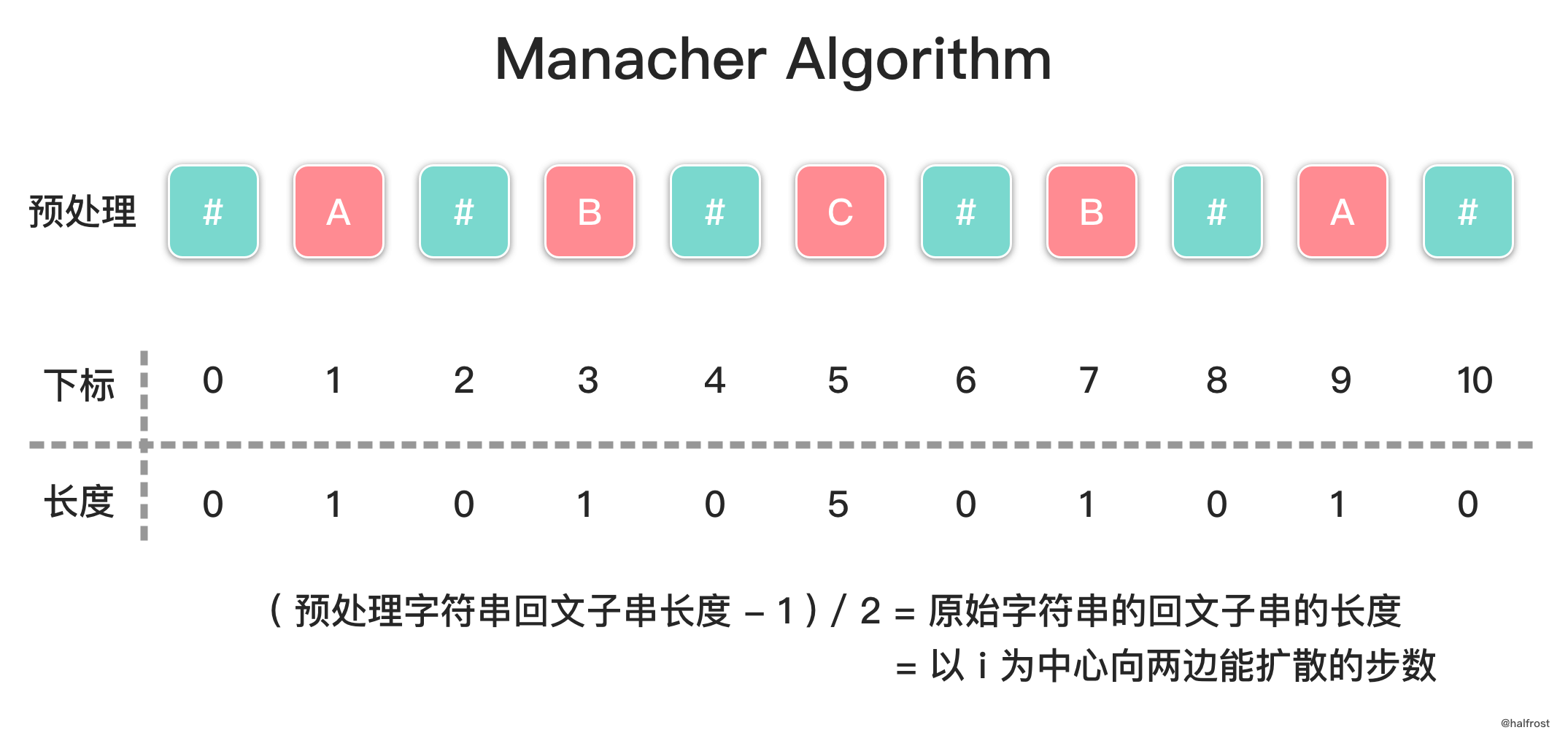
首先是预处理,向字符串的头尾以及每两个字符中间添加一个特殊字符
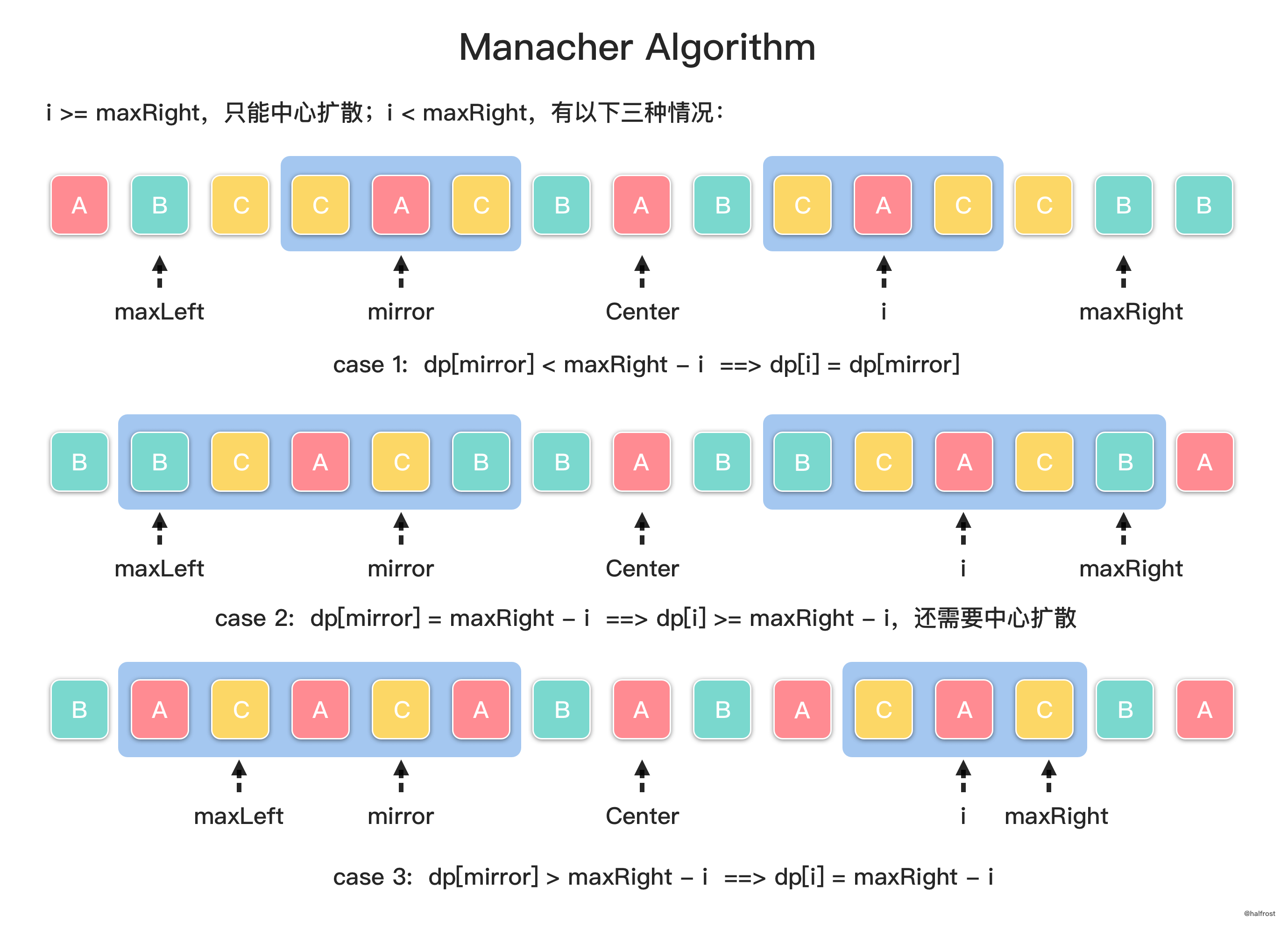
#,比如字符串aaba处理后会变成#a#a#b#a#。那么原先长度为偶数的回文字符串aa会变成长度为奇数的回文字符串#a#a#,而长度为奇数的回文字符串aba会变成长度仍然为奇数的回文字符串#a#b#a#,经过预处理以后,都会变成长度为奇数的字符串。**注意这里的特殊字符不需要是没有出现过的字母,也可以使用任何一个字符来作为这个特殊字符。**这是因为,当我们只考虑长度为奇数的回文字符串时,每次我们比较的两个字符奇偶性一定是相同的,所以原来字符串中的字符不会与插入的特殊字符互相比较,不会因此产生问题。**预处理以后,以某个中心扩散的步数和实际字符串长度是相等的。**因为半径里面包含了插入的特殊字符,又由于左右对称的性质,所以扩散半径就等于原来回文子串的长度。核心部分是如何通过左边已经扫描过的数据推出右边下一次要扩散的中心。这里定义下一次要扩散的中心下标是
i。如果i比maxRight要小,只能继续中心扩散。如果i比maxRight大,这是又分为 3 种情况。三种情况见上图。将上述 3 种情况总结起来,就是 :dp[i] = min(maxRight-i, dp[2*center-i]),其中,mirror相对于center是和i中心对称的,所以它的下标可以计算出来是2*center-i。更新完dp[i]以后,就要进行中心扩散了。中心扩散以后动态维护最长回文串并相应的更新center,maxRight,并且记录下原始字符串的起始位置begin和maxLen。
package leetcode // 解法一 Manacher's algorithm,时间复杂度 O(n),空间复杂度 O(n)funclongestPalindrome(sstring) string { iflen(s) <2 { returns } newS:=make([]rune, 0) newS=append(newS, '#') for_, c:=ranges { newS=append(newS, c) newS=append(newS, '#') } // dp[i]: 以预处理字符串下标 i 为中心的回文半径(奇数长度时不包括中心)// maxRight: 通过中心扩散的方式能够扩散的最右边的下标// center: 与 maxRight 对应的中心字符的下标// maxLen: 记录最长回文串的半径// begin: 记录最长回文串在起始串 s 中的起始下标dp, maxRight, center, maxLen, begin:=make([]int, len(newS)), 0, 0, 1, 0fori:=0; i<len(newS); i++ { ifi<maxRight { // 这一行代码是 Manacher 算法的关键所在dp[i] =min(maxRight-i, dp[2*center-i]) } // 中心扩散法更新 dp[i]left, right:=i-(1+dp[i]), i+(1+dp[i]) forleft>=0&&right<len(newS) &&newS[left] ==newS[right] { dp[i]++left--right++ } // 更新 maxRight,它是遍历过的 i 的 i + dp[i] 的最大者ifi+dp[i] >maxRight { maxRight=i+dp[i] center=i } // 记录最长回文子串的长度和相应它在原始字符串中的起点ifdp[i] >maxLen { maxLen=dp[i] begin= (i-maxLen) /2// 这里要除以 2 因为有我们插入的辅助字符 # } } returns[begin : begin+maxLen] } funcmin(x, yint) int { ifx<y { returnx } returny } // 解法二 滑动窗口,时间复杂度 O(n^2),空间复杂度 O(1)funclongestPalindrome1(sstring) string { iflen(s) ==0 { return"" } left, right, pl, pr:=0, -1, 0, 0forleft<len(s) { // 移动到相同字母的最右边(如果有相同字母)forright+1<len(s) &&s[left] ==s[right+1] { right++ } // 找到回文的边界forleft-1>=0&&right+1<len(s) &&s[left-1] ==s[right+1] { left--right++ } ifright-left>pr-pl { pl, pr=left, right } // 重置到下一次寻找回文的中心left= (left+right)/2+1right=left } returns[pl : pr+1] } // 解法三 中心扩散法,时间复杂度 O(n^2),空间复杂度 O(1)funclongestPalindrome2(sstring) string { res:=""fori:=0; i<len(s); i++ { res=maxPalindrome(s, i, i, res) res=maxPalindrome(s, i, i+1, res) } returnres } funcmaxPalindrome(sstring, i, jint, resstring) string { sub:=""fori>=0&&j<len(s) &&s[i] ==s[j] { sub=s[i : j+1] i--j++ } iflen(res) <len(sub) { returnsub } returnres } // 解法四 DP,时间复杂度 O(n^2),空间复杂度 O(n^2)funclongestPalindrome3(sstring) string { res, dp:="", make([][]bool, len(s)) fori:=0; i<len(s); i++ { dp[i] =make([]bool, len(s)) } fori:=len(s) -1; i>=0; i-- { forj:=i; j<len(s); j++ { dp[i][j] = (s[i] ==s[j]) && ((j-i<3) ||dp[i+1][j-1]) ifdp[i][j] && (res==""||j-i+1>len(res)) { res=s[i : j+1] } } } returnres }