回溯法(backtrack)常用于遍历列表所有子集,是 DFS 深度搜索一种,一般用于全排列,穷尽所有可能,遍历的过程实际上是一个决策树的遍历过程。时间复杂度一般 O(N!),它不像动态规划存在重叠子问题可以优化,回溯算法就是纯暴力穷举,复杂度一般都很高。
result= [] funcbacktrack(选择列表,路径): if满足结束条件: result.add(路径) returnfor选择in选择列表: 做选择backtrack(选择列表,路径) 撤销选择核心就是从选择列表里做一个选择,然后一直递归往下搜索答案,如果遇到路径不通,就返回来撤销这次选择。
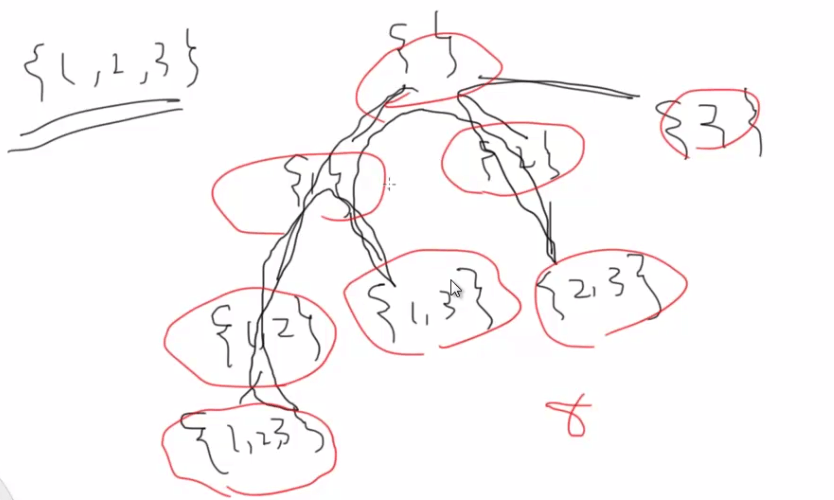
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
遍历过程
classSolution: defsubsets(self, nums: List[int]) ->List[List[int]]: n=len(nums) result= [] defbacktrack(start, k, route=[]): iflen(route) ==k: result.append(route.copy()) returnforiinrange(start, n): route.append(nums[i]) backtrack(i+1, k) route.pop() returnforkinrange(n+1): backtrack(0, k) returnresult给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。说明:解集不能包含重复的子集。
classSolution: defsubsetsWithDup(self, nums: List[int]) ->List[List[int]]: nums=sorted(nums) n=len(nums) result= [] defbacktrack(start, k, route=[]): iflen(route) ==k: result.append(route.copy()) returnlast=Noneforiinrange(start, n): ifnums[i] !=last: route.append(nums[i]) backtrack(i+1, k) last=route.pop() returnforkinrange(n+1): backtrack(0, k) returnresult给定一个没有重复数字的序列,返回其所有可能的全排列。
- 思路 1:需要记录已经选择过的元素,满足条件的结果才进行返回,需要额外 O(n) 的空间
classSolution: defpermute(self, nums: List[int]) ->List[List[int]]: n=len(nums) result= [] in_route= [False] *ndefbacktrack(route=[]): iflen(route) ==n: result.append(route.copy()) returnforiinrange(n): ifnotin_route[i]: route.append(nums[i]) in_route[i] =Truebacktrack() route.pop() in_route[i] =Falsereturnbacktrack() returnresult- 思路 2: 针对此题的更高级的回溯,利用原有的数组,每次回溯将新选择的元素与当前位置元素交换,回溯完成再换回来
classSolution: defpermute(self, nums: List[int]) ->List[List[int]]: n=len(nums) result= [] defbacktrack(idx=0): ifidx==n: result.append(nums.copy()) foriinrange(idx, n): nums[idx], nums[i] =nums[i], nums[idx] backtrack(idx+1) nums[idx], nums[i] =nums[i], nums[idx] returnbacktrack() returnresult给定一个可包含重复数字的序列,返回所有不重复的全排列。
注意此题(貌似)无法使用上题的思路 2,因为交换操作会打乱排序。
classSolution: defpermuteUnique(self, nums: List[int]) ->List[List[int]]: nums=sorted(nums) n=len(nums) result= [] in_route= [False] *ndefbacktrack(route=[]): iflen(route) ==n: result.append(route.copy()) returnlast=Noneforiinrange(n): ifnotin_route[i] andnums[i] !=last: route.append(nums[i]) in_route[i] =Truebacktrack() last=route.pop() in_route[i] =Falsereturnbacktrack() returnresultclassSolution: defcombinationSum(self, candidates: List[int], target: int) ->List[List[int]]: n=len(candidates) result= [] defbacktrack(first=0, route=[], route_sum=0): ifroute_sum==target: result.append(route.copy()) returnifroute_sum>target: returnforiinrange(first, n): route.append(candidates[i]) route_sum+=candidates[i] backtrack(i, route, route_sum) route_sum-=route.pop() returnbacktrack() returnresultclassSolution: defletterCombinations(self, digits: str) ->List[str]: n=len(digits) result= [] ifn==0: returnresultnum2char= { '2': ['a', 'b', 'c'], '3': ['d', 'e', 'f'], '4': ['g', 'h', 'i'], '5': ['j', 'k', 'l'], '6': ['m', 'n', 'o'], '7': ['p', 'q', 'r', 's'], '8': ['t', 'u', 'v'], '9': ['w', 'x', 'y', 'z'] } defbacktrack(idx=0, route=[]): ifidx==n: result.append(''.join(route)) returnforcinnum2char[digits[idx]]: route.append(c) backtrack(idx+1, route) route.pop() returnbacktrack() returnresultclassSolution: defpartition(self, s: str) ->List[List[str]]: N=len(s) Pal=collections.defaultdict(set) defisPal(i, j): ifi<j: returnjinPal[i] returnTrueforjinrange(N): foriinrange(j+1): ifs[i] ==s[j] andisPal(i+1, j-1): Pal[i].add(j) result= [] defbacktrack(first=0, route=[]): iffirst==N: result.append(route[:]) returnforiinPal[first]: route.append(s[first:i+1]) backtrack(i+1) route.pop() returnbacktrack() returnresultclassSolution: defrestoreIpAddresses(self, s: str) ->List[str]: n=len(s) result= [] ifn>12: returnresultdefValid_s(i, j): returni<jandj<=nand ((s[i] !='0'andint(s[i:j]) <256) or (s[i] =='0'andi==j-1)) defbacktrack(start=0, route=[]): iflen(route) ==3: ifValid_s(start, n): result.append('.'.join(route) +'.'+s[start:]) returnforiinrange(start, start+3): ifValid_s(start, i+1): route.append(s[start:i+1]) backtrack(i+1, route) route.pop() returnbacktrack() returnresult