124.binary-tree-maximum-path-sum.md

题目地址(124. 二叉树中的最大路径和)

https://leetcode-cn.com/problems/binary-tree-maximum-path-sum/description/

题目描述

 给定一个非空二叉树，返回其最大路径和。 本题中，路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。 示例 1： 输入：[1,2,3] 1 / \ 2 3 输出：6 示例 2： 输入：[-10,9,20,null,null,15,7]   -10    / \   9  20     /  \    15   7 输出：42 

前置知识

• 树

公司

• 阿里
• 腾讯
• 百度
• 字节

思路

这道题目的 path 让我误解了，然后浪费了很多时间来解这道题。我觉得 leetcode 给的 demo 太少了，不足以让我理解 path 的概念因此我这里自己画了一个图，来补充一下，帮助大家理解 path 的概念，不要像我一样理解错啦。

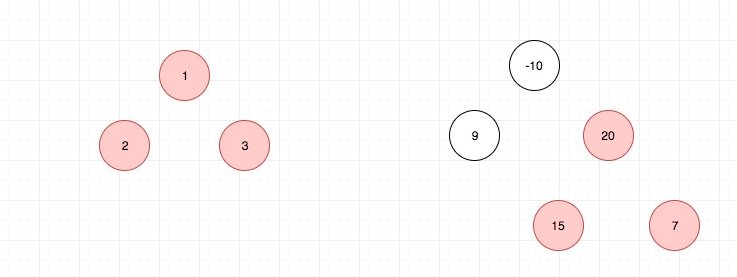
首先是官网给的两个例子：

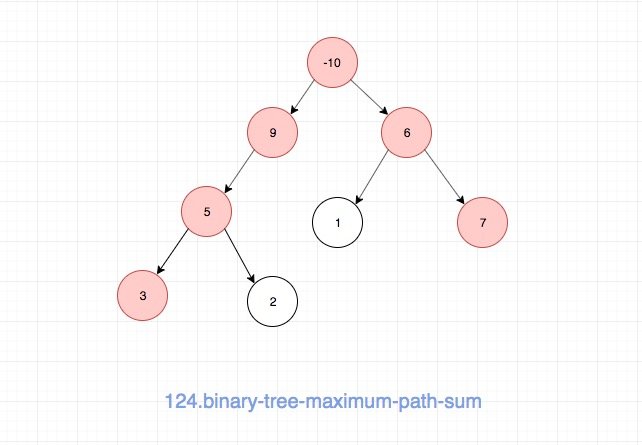
接着是我自己画的一个例子：

如图红色的部分是最大路径上的节点。大家可以结合上面的 demo 来继续理解一下 path， 除非你理解了 path，否则不要往下看。

树的题目，基本都是考察递归思想的。因此我们需要思考如何去定义我们的递归函数，在这里我定义了一个递归函数，它的功能是，返回以当前节点为根节点的MaxPath

但是有两个条件:

1. 根节点必须选择
2. 左右子树只能选择一个

为什么要有这两个条件?

我的想法是原问题可以转化为：以每一个节点为根节点，分别求出 MaxPath，最后计算最大值，因此第一个条件需要满足.

对于第二个条件，由于递归函数子节点的返回值会被父节点使用，因此我们如果两个孩子都选择了就不符合 MaxPath 的定义了。实际上这道题，当遍历到某一个节点的时候，我们需要子节点的信息，然后同时结合自身的 val 来决定要不要选取左右子树以及选取的话要选哪一个， 因此这个过程本质上就是后序遍历

基本算法就是不断调用递归函数，然后在调用过程中不断计算和更新 MaxPath，最后在主函数中将 MaxPath 返回即可。

关键点解析

• 递归
• 理解题目中的 path 定义

代码

代码支持：JavaScript，Java，Python, CPP

• JavaScript

/* * @lc app=leetcode id=124 lang=javascript * * [124] Binary Tree Maximum Path Sum *//** * Definition for a binary tree node. * function TreeNode(val) { * this.val = val; * this.left = this.right = null; * } */functionhelper(node,payload){if(node===null)return0;constl=helper(node.left,payload);constr=helper(node.right,payload);payload.max=Math.max(node.val+Math.max(0,l)+Math.max(0,r),payload.max);returnnode.val+Math.max(l,r,0);}/** * @param {TreeNode} root * @return {number} */varmaxPathSum=function(root){if(root===null)return0;constpayload={max: root.val,};helper(root,payload);returnpayload.max;};

• Java

/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */classSolution { intans; publicintmaxPathSum(TreeNoderoot) { ans = Integer.MIN_VALUE; helper(root); // recursionreturnans; } publicinthelper(TreeNoderoot) { if (root == null) return0; intleftMax = Math.max(0, helper(root.left)); // find the max sub-path sum in left sub-treeintrightMax = Math.max(0, helper(root.right)); // find the max sub-path sum in right sub-treeans = Math.max(ans, leftMax+rightMax+root.val); // find the max path sum at current nodereturnmax(leftMax, rightMax) + root.val; // according to the definition of path, the return value of current node can only be that the sum of current node value plus either left or right max path sum. } }

• Python

classSolution: ans=float('-inf') defmaxPathSum(self, root: TreeNode) ->int: defhelper(node): ifnotnode: return0l=helper(node.left) r=helper(node.right) self.ans=max(self.ans, max(l,0) +max(r, 0) +node.val) returnmax(l, r, 0) +node.valhelper(root) returnself.ans

• CPP

classSolution { private:int ans = INT_MIN; intpostOrder(TreeNode *root) { if (!root) return INT_MIN; int L = max(0, postOrder(root->left)), R = max(0, postOrder(root->right)); ans = max(ans, L + R + root->val); return root->val + max(L, R); } public:intmaxPathSum(TreeNode* root) { postOrder(root); return ans; } }; 

复杂度分析

• 时间复杂度：$O(n)$，其中 n 为节点数。
• 空间复杂度：$O(h)$， 其中 h 为树高。

相关题目

• 113.path-sum-ii

大家对此有何看法，欢迎给我留言，我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 37K star 啦。 大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。