101.symmetric-tree.md

题目地址(101. 对称二叉树)

https://leetcode-cn.com/problems/symmetric-tree/

题目描述

给定一个二叉树，检查它是否是镜像对称的。   例如，二叉树 [1,2,2,3,4,4,3] 是对称的。 1 / \ 2 2 / \ / \ 3 4 4 3   但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的: 1 / \ 2 2 \ \ 3 3   进阶： 你可以运用递归和迭代两种方法解决这个问题吗？ 

公司

• 阿里
• 腾讯
• 百度
• 字节
• bloomberg
• linkedin
• microsoft

前置知识

• 二叉树
• 递归

思路

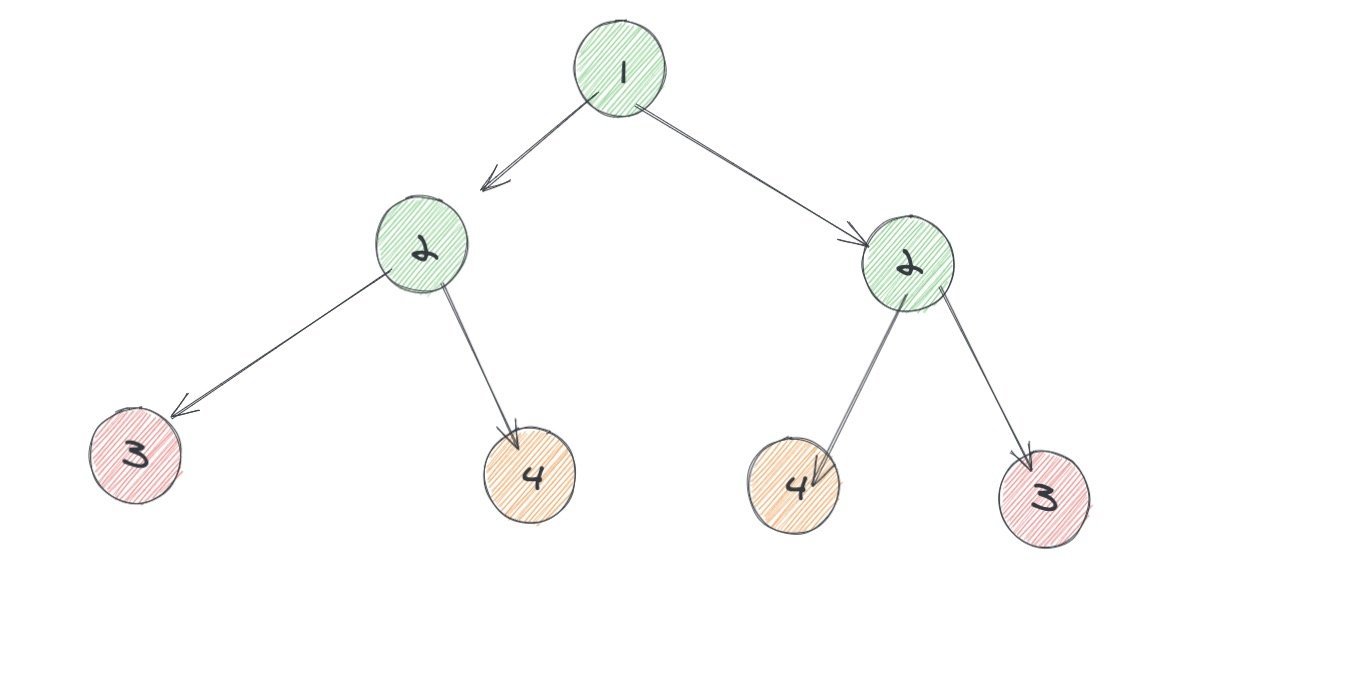
看到这题的时候，我的第一直觉是 DFS。然后我就想:如果左子树是镜像，并且右子树也是镜像，是不是就说明整体是镜像？。经过几秒的思考， 这显然是不对的，不符合题意。

很明显其中左子树中的节点会和右子树中的节点进行比较，我把比较的元素进行了颜色区分，方便大家看。

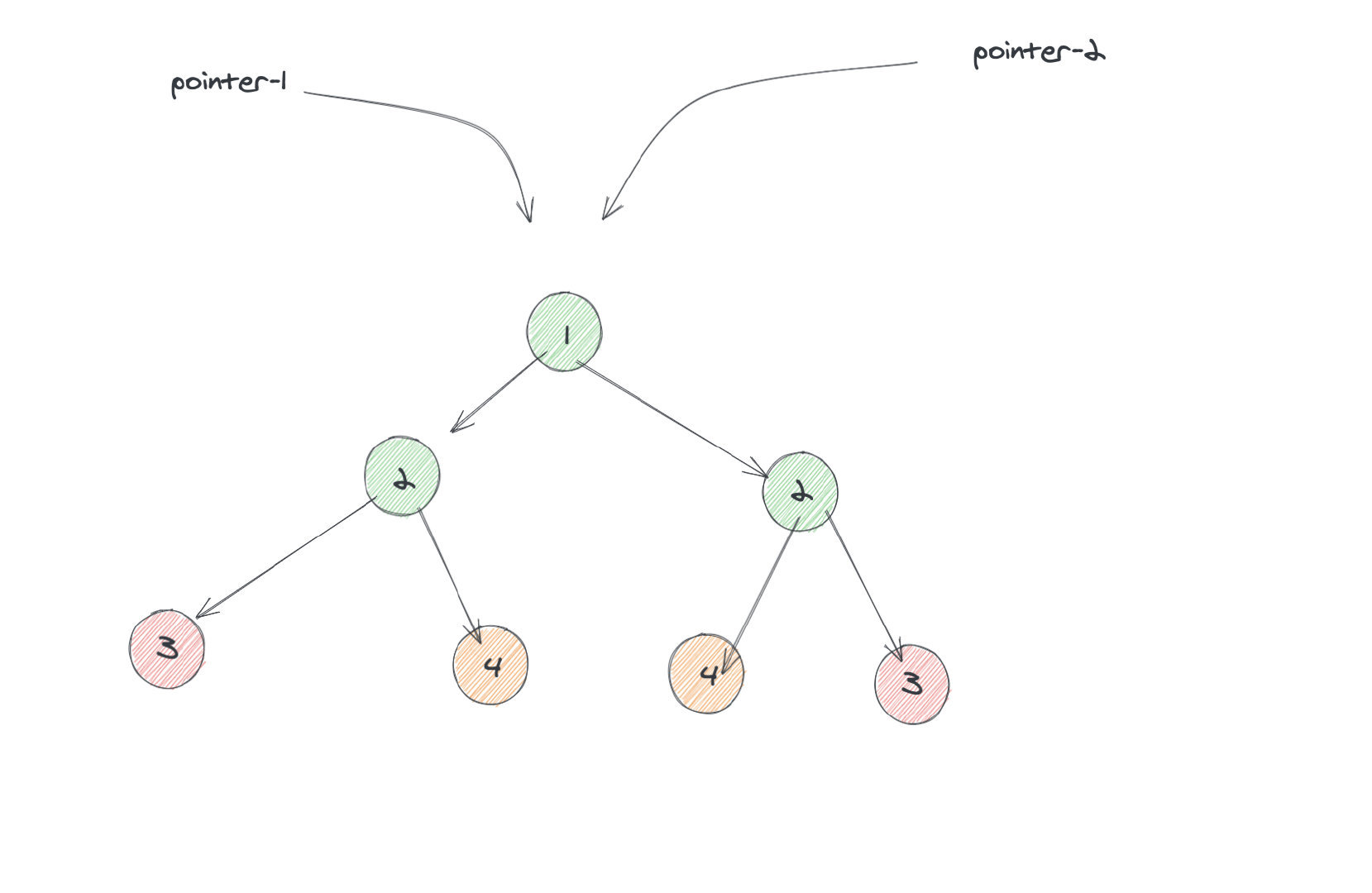
这里我的想法是：遍历每一个节点的时候，如果我都可以通过某种方法知道它对应的对称节点是谁，这样的话我直接比较两者是否一致就行了。

因此想法是两次遍历，第一次遍历的同时将遍历结果存储到哈希表中，然后第二次遍历去哈希表取。这种方法可行，但是需要 N 的空间（N 为节点总数）。我想到如果两者可以同时进行遍历，是不是就省去了哈希表的开销。

如果不明白的话，我举个简单例子：

给定一个数组，检查它是否是镜像对称的。例如，数组 [1,2,2,3,2,2,1] 是对称的。 

如果用哈希表的话大概是：

seen=dict() fori, numinenumerate(nums): seen[i] =numfori, numinenumerate(nums): ifseen[len(nums) -1-i] !=num: returnFalsereturnTrue

而同时遍历的话大概是这样的：

l=0r=len(nums) -1whilel<r: ifnums[l] !=nums[r]: returnFalsel+=1r-=1returnTrue

其实更像本题一点的话应该是从中间分别向两边扩展 😂

代码

代码支持：C++, Java, Python3

C++ Code:

/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * };*/classSolution { public:boolisSymmetric(TreeNode* root) { return root==NULL?true:recur(root->left, root->right); } boolrecur(TreeNode* l, TreeNode* r) { if(l == NULL && r==NULL) { returntrue; } // 只存在一个子节点 或者左右不相等if(l==NULL || r==NULL || l->val != r->val) { returnfalse; } returnrecur(l->left, r->right) && recur(l->right, r->left); } };

Java Code:

/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */classSolution { publicbooleanisSymmetric(TreeNoderoot) { if(root == null) { returntrue; } else{ returnrecur(root.left, root.right); } // return root == null ? true : recur(root.left, root.right); } publicbooleanrecur(TreeNodel, TreeNoder) { if(l == null && r==null) { returntrue; } // 只存在一个子节点 或者左右不相等if(l==null || r==null || l.val != r.val) { returnfalse; } returnrecur(l.left, r.right) && recur(l.right, r.left); } }

Python3 Code:

classSolution: defisSymmetric(self, root: TreeNode) ->bool: defdfs(root1, root2): ifroot1==root2==None: returnTrueifnotroot1ornotroot2: returnFalseifroot1.val!=root2.val: returnFalsereturndfs(root1.left, root2.right) anddfs(root1.right, root2.left) ifnotroot: returnTruereturndfs(root.left, root.right)

复杂度分析

• 时间复杂度：$O(N)$，其中 N 为节点数。
• 空间复杂度：递归的深度最高为节点数，因此空间复杂度是 $O(N)$，其中 N 为节点数。

大家对此有何看法，欢迎给我留言，我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 37K star 啦。 大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。