我们从二叉树的根节点 root 开始进行深度优先搜索。
在遍历中的每个节点处,我们输出 D 条短划线(其中 D 是该节点的深度),然后输出该节点的值。(如果节点的深度为 D,则其直接子节点的深度为 D + 1。根节点的深度为 0)。
如果节点只有一个子节点,那么保证该子节点为左子节点。
给出遍历输出 S,还原树并返回其根节点 root。
示例 1:
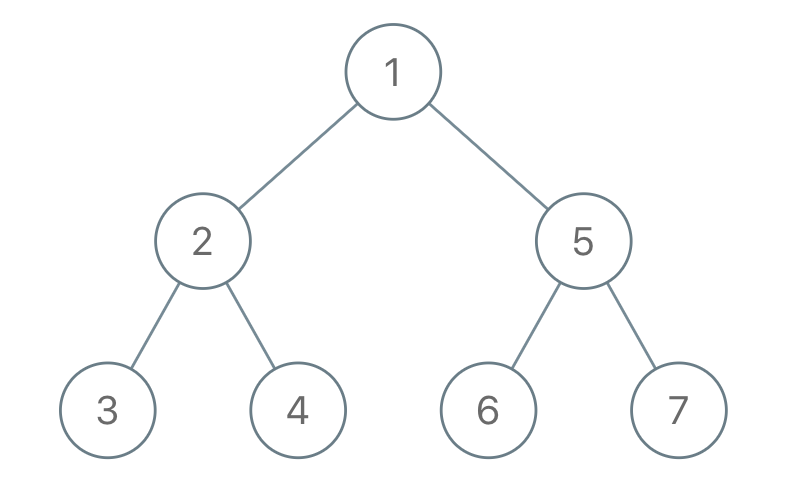
输入:"1-2--3--4-5--6--7" 输出:[1,2,5,3,4,6,7] 示例 2:
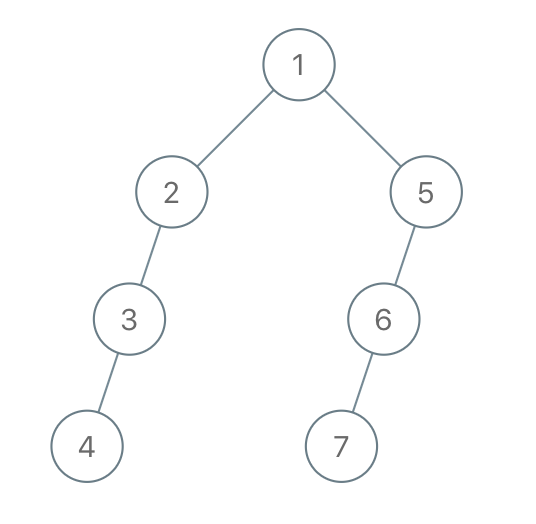
输入:"1-2--3---4-5--6---7" 输出:[1,2,5,3,null,6,null,4,null,7] 示例 3:
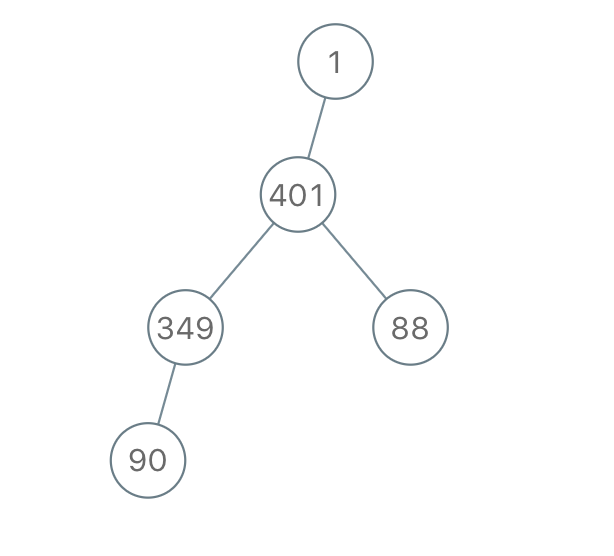
输入:"1-401--349---90--88" 输出:[1,401,null,349,88,90] 提示:
- 原始树中的节点数介于
1和1000之间。 - 每个节点的值介于
1和10 ^ 9之间。
标签: 树、深度优先搜索
主要就是根据先序遍历如何把树构建出来,其最主要就是找到当前待插入节点它爹,优先插入到它爹的左子节点,我们可以用一个链表来做辅助,该链表索引代表层级,元素存放其节点,由于是先序遍历(根-左-右),也就是右覆盖左时,此时左树已遍历完成,故无需考虑覆盖问题,利用该链表,我们根据层级便可轻松找到它爹,具体如下所示:
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */publicclassSolution { publicTreeNoderecoverFromPreorder(StringS) { char[] chars = S.toCharArray(); intlen = chars.length; List<TreeNode> levels = newLinkedList<>(); for (inti = 0; i < len; ) { intlevel = 0, val = 0; while (chars[i] == '-') { // 获取所在层级,Character.isDigit() 会比较慢 ++i; ++level; } while (i < len && chars[i] != '-') { // 获取节点的值val = val * 10 + chars[i++] - '0'; } TreeNodecurNode = newTreeNode(val); if (level > 0) { TreeNodeparent = levels.get(level - 1); if (parent.left == null) { // 如果节点只有一个子节点,那么保证该子节点为左子节点。parent.left = curNode; } else { parent.right = curNode; } } levels.add(level, curNode); // 因为是先序遍历(根-左-右),也就是右覆盖左时,此时左树已遍历完成,故无需考虑覆盖问题 } returnlevels.get(0); } }基于上面的思路,其实我们没有必要把所有层级都保存下来,由于是先序遍历,在找待插入节点它爹时,我们可以把不小于它层级的元素都删除,基于此,用一个辅助栈便可完成寻爹之旅,具体如下所示:
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */publicclassSolution { publicTreeNoderecoverFromPreorder(StringS) { char[] chars = S.toCharArray(); intlen = chars.length; LinkedList<TreeNode> stack = newLinkedList<>(); for (inti = 0; i < len; ) { intlevel = 0, val = 0; while (chars[i] == '-') { // 获取所在层级,Character.isDigit() 会比较慢 ++i; ++level; } while (i < len && chars[i] != '-') { // 获取节点的值val = val * 10 + chars[i++] - '0'; } TreeNodecurNode = newTreeNode(val); while (stack.size() > level) { // 栈顶不是父亲,栈顶出栈stack.removeLast(); } if (level > 0) { TreeNodeparent = stack.getLast(); if (parent.left == null) { // 如果节点只有一个子节点,那么保证该子节点为左子节点。parent.left = curNode; } else { parent.right = curNode; } } stack.addLast(curNode); } returnstack.get(0); } }如果你同我一样热爱数据结构、算法、LeetCode,可以关注我 GitHub 上的 LeetCode 题解:awesome-java-leetcode