Appendix Fuzzy Operator Formulas The following is a list of formulas used to operate on the membership grades of fuzzy set A for selected general operations on fuzzy sets. In the following formulas, xn represents the new membership grades after applying the operators, and yn represents the original membership grades for the elements of fuzzy set A Concentrate  Dilate  Intensify Contrast  Normalize  Complement Standard  Sugeno[ ],w ],w 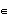 (-1, (-1, 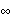 ) )  Yager[w], w 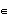 (0, (0, 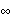 ) )  Intersection Formulas The following is a list of the formulas used for various intersections between two fuzzy sets, A and B. The following formulas indicate how the membership grades for corresponding elements in fuzzy sets A and B should be combined. In the formulas, a represents the membership grade for an element in fuzzy set A, and b represents the membership grade for an element in fuzzy set B. Standard  Hamacher[v], v 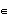 (0, (0, 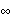 ) )  Frank[s], s 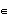 (0, (0, 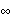 ) ) 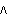 s s 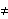 1. 1.  Yager[w], w 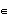 (0, (0, 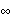 ) )  DuboisPrade[ ], ],  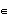 [0, 1] [0, 1]  Dombi[ ], ],  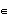 (0, (0, 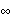 ) )  Weber[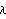 ], ], 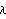 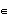 (-1, (-1, 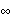 ) )  Yu[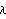 ], ], 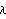 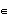 (-1 , (-1 , 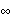 ) )  Union Formulas The following is a list of the formulas used for various unions between two fuzzy sets, A and B. The following formulas indicate how the membership grades for corresponding elements in fuzzy sets A and B should be combined. In the formulas, a represents the membership grade for an element in fuzzy set A, and b represents the membership grade for the corresponding element in fuzzy set B. Standard  Hamacher[v], v 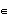 (0, (0, 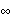 ) )  Frank[s], s 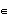 (0, (0, 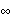 ) ) 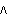 s s 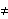 1 1  Yager[w], w 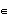 (0, (0, 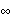 ) )  DuboisPrade[ ], ],  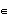 [0, 1] [0, 1]  Dombi[ ], ],  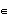 (0, (0, 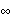 ) )  Weber[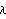 ], ], 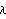 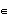 (-1 , (-1 , 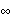 ) )  Yu[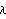 ], ], 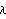 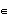 (-1 , (-1 , 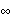 ) )  Averaging Formulas Following is a list of the formulas for taking the various averages used in this package. The averaging operations are denoted by the letter h, and  represent the membership grades for corresponding elements in the n fuzzy sets being averaged. represent the membership grades for corresponding elements in the n fuzzy sets being averaged. Arithmetic Mean  Geometric Mean  Harmonic Mean  Generalized Mean[ ], ],  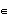 (- (-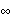 , ,  ) )  Miscellaneous Formulas Gaussian Fuzzy Sets  where m is the mean, s is the width, and x is the element. Bell Fuzzy Sets  where c is the center, crossover points are at c ± w, a slope at the crossover points of s/2w, and x is the element. Sigmoid Fuzzy Sets  where s controls the slope at crossover point c, and x is the element. |