https://leetcode-cn.com/problems/decode-string/
给定一个经过编码的字符串,返回它解码后的字符串。 编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。 你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。 此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。 示例 1: 输入:s = "3[a]2[bc]" 输出:"aaabcbc" 示例 2: 输入:s = "3[a2[c]]" 输出:"accaccacc" 示例 3: 输入:s = "2[abc]3[cd]ef" 输出:"abcabccdcdcdef" 示例 4: 输入:s = "abc3[cd]xyz" 输出:"abccdcdcdxyz" - 栈
- 括号匹配
题目要求将一个经过编码的字符解码并返回解码后的字符串。题目给定的条件是只有四种可能出现的字符
- 字母
- 数字
- [
- ]
并且输入的方括号总是满足要求的(成对出现),数字只表示重复次数。
那么根据以上条件,可以看出其括号符合栈先进后出的特性以及递归的特质,稍后我们使用递归来解。
那么现在看一下迭代的解法。
我们可以利用 stack 来实现这个操作,遍历这个字符串 s,判断每一个字符的类型:
- 如果是字母 --> 添加到 stack 当中
- 如果是数字 --> 先不着急添加到 stack 中 --> 因为有可能有多位
- 如果是 [ --> 说明重复字符串开始 --> 将数字入栈 --> 并且将数字清零
- 如果是 ] --> 说明重复字符串结束 --> 将重复字符串重复前一步储存的数字遍
拿题目给的例子s = "3[a2[c]]" 来说:
在遇到 】 之前,我们不断执行压栈操作:
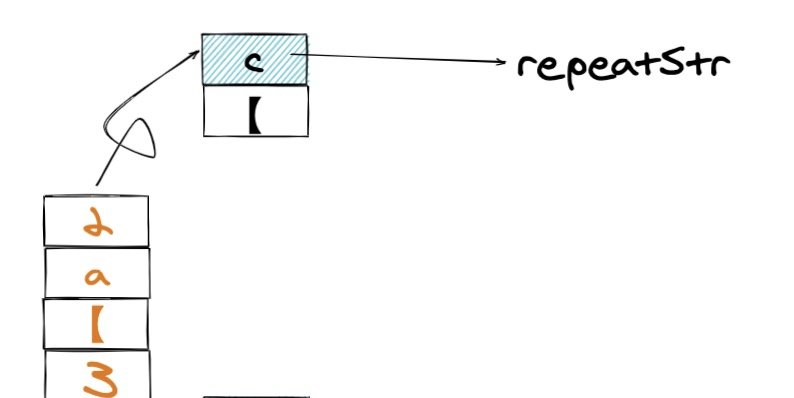
当遇到 】的时候,说明我们应该出栈了,不断出栈知道对应的【,这中间的就是 repeatStr。
但是要重复几次呢? 我们需要继续出栈,直到非数字为止,这个数字我们记录为 repeatCount。
而最终的字符串就是 repeatCount 个 repeatStr 拼接的形式。 并将其看成一个字母压入栈中。
继续,后面的逻辑是一样的:
(最终图)
代码支持:Python
Python:
classSolution: defdecodeString(self, s: str) ->str: stack= [] forcins: ifc==']': repeatStr=''repeatCount=''whilestackandstack[-1] !='[': repeatStr=stack.pop() +repeatStr# pop 掉 "["stack.pop() whilestackandstack[-1].isnumeric(): repeatCount=stack.pop() +repeatCountstack.append(repeatStr*int(repeatCount)) else: stack.append(c) return"".join(stack)复杂度分析
- 时间复杂度:$O(N)$,其中 N 为解码后的 s 的长度。
- 空间复杂度:$O(N)$,其中 N 为解码后的 s 的长度。
递归的解法也是类似。由于递归的解法并不比迭代书写简单,以及递归我们将在第三节讲述。
主逻辑仍然和迭代一样。 只不过每次碰到左括号就进入递归,碰到右括号就跳出递归返回即可。
唯一需要注意的是,我这里使用了 start 指针跟踪当前遍历到的位置, 因此如果使用递归需要在递归返回后更新指针。
classSolution: defdecodeString(self, s: str) ->str: defdfs(start): repeat_str=repeat_count=''whilestart<len(s): ifs[start].isnumeric(): repeat_count+=s[start] elifs[start] =='[': # 更新指针start, t_str=dfs(start+1) # repeat_count 仅作用于 t_str,而不作用于当前的 repeat_strrepeat_str=repeat_str+t_str*int(repeat_count) repeat_count=''elifs[start] ==']': returnstart, repeat_strelse: repeat_str+=s[start] start+=1returnrepeat_strreturndfs(0)复杂度分析
- 时间复杂度:$O(N)$,其中 N 为解码后的 s 的长度。
- 空间复杂度:$O(N)$,其中 N 为解码后的 s 的长度。
更多题解可以访问我的 LeetCode 题解仓库:https://github.com/azl397985856/leetcode 。 目前已经 37K star 啦。
大家也可以关注我的公众号《力扣加加》获取更多更新鲜的 LeetCode 题解