Skip to content

Latest commit

 

History

History
159 lines (116 loc) · 4.47 KB

11.container-with-most-water.md

File metadata and controls

159 lines (116 loc) · 4.47 KB

题目地址(11. 盛最多水的容器)

https://leetcode-cn.com/problems/container-with-most-water/description/

题目描述

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点  (i, ai) 。在坐标内画 n 条垂直线，垂直线 i  的两个端点分别为  (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与  x  轴共同构成的容器可以容纳最多的水。 说明：你不能倾斜容器，且  n  的值至少为 2。 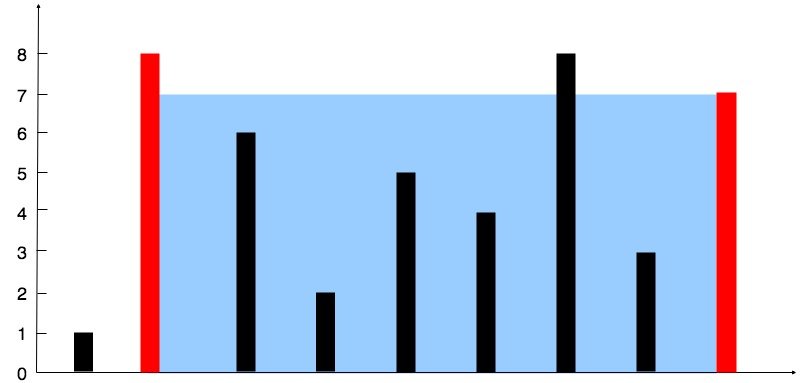![11.container-with-most-water-question](https://p.ipic.vip/ia6rj3.jpg) 图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为  49。 示例： ` 输入：[1,8,6,2,5,4,8,3,7] 输出：49

前置知识

  • 双指针

公司

  • 字节
  • 腾讯
  • 百度
  • 阿里

思路

题目中说找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。 ，因此符合直觉的解法就是固定两个端点，计算可以承载的水量， 然后不断更新最大值，最后返回最大值即可。这种算法，需要两层循环，时间复杂度是 $O(n^2)$。

代码（JS）:

letmax=0;for(leti=0;i<height.length;i++){for(letj=i+1;j<height.length;j++){constcurrentArea=Math.abs(i-j)*Math.min(height[i],height[j]);if(currentArea>max){max=currentArea;}}}returnmax;

虽然解法效率不高，但是可以通过（JS 可以通过，Python 不可以，其他语言没有尝试）。那么有没有更优的解法呢？

我们来换个角度来思考这个问题，上述的解法是通过两两组合，这无疑是完备的。我们换个角度思考，是否可以:

  • 先计算长度为 n 的面积
  • 然后计算长度为 n-1 的面积
  • ...
  • 计算长度为 1 的面积。

很显然这种解法也是完备的，但是似乎时间复杂度还是 $O(n ^ 2)$, 不要着急，我们继续优化。

考虑一下，如果我们计算 n-1 长度的面积的时候，是可以直接排除一半的结果的。

如图：

11.container-with-most-water

比如我们计算 n 面积的时候，假如左侧的线段高度比右侧的高度低，那么我们通过左移右指针来将长度缩短为 n - 1 的做法是没有意义的，因为新形成的面积变成了(n-1) * heightOfLeft， 这个面积一定比刚才的长度为 n 的面积 （n * heightOfLeft） 小。

也就是说最大面积一定是当前的面积或者通过移动短的端点得到。

关键点解析

  • 双指针优化时间复杂度

代码

  • 语言支持：JS，C++,Python

JavaScript Code:

/** * @param {number[]} height * @return {number} */varmaxArea=function(height){if(!height||height.length<=1)return0;letleftPos=0;letrightPos=height.length-1;letmax=0;while(leftPos<rightPos){constcurrentArea=Math.abs(leftPos-rightPos)*Math.min(height[leftPos],height[rightPos]);if(currentArea>max){max=currentArea;}// 更新小的if(height[leftPos]<height[rightPos]){leftPos++;}else{// 如果相等就随便了rightPos--;}}returnmax;};

C++ Code:

classSolution { public:intmaxArea(vector<int>& height) { auto ret = 0ul, leftPos = 0ul, rightPos = height.size() - 1; while( leftPos < rightPos) { ret = std::max(ret, std::min(height[leftPos], height[rightPos]) * (rightPos - leftPos)); if (height[leftPos] < height[rightPos]) ++leftPos; else --rightPos; } return ret; } };

Python Code:

classSolution: defmaxArea(self, heights): l, r=0, len(heights) -1ans=0whilel<r: ans=max(ans, (r-l) *min(heights[l], heights[r])) ifheights[r] >heights[l]: l+=1else: r-=1returnans

复杂度分析

  • 时间复杂度：由于左右指针移动的次数加起来正好是 n， 因此时间复杂度为 $O(N)$。
  • 空间复杂度：$O(1)$。

更多题解可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 37K star 啦。

关注公众号力扣加加，努力用清晰直白的语言还原解题思路，并且有大量图解，手把手教你识别套路，高效刷题。

close